Babylónská perioda
Úvod
Babylónská perioda je výrazná perioda pohybu vnitřních planet. Činí přibližně B=427 let.
Odkazy
Ray Tomes
Ray Tomes zahrnul Babylonskou periodu do svých schemat (viz Teoretické periody cyklů ):
427.0 213.5 106.8 53.38 26.69
142.3 71.17 35.59 17.79 8.897 4.448 2.224
Timo Niroma
1. 415-425 let
2. 305-314 let
3. 260-280 let, uvlivňuje vlhkost
4. 177-227 let, téměř vše, velmi výrazný,
silný cyklus, ovlivňuje teplotu
(medián 202 let)
5. 154-157 let, delší cyklus, 13 Jupiterových let
6. 143-148 let, delší cyklus, 13 průměrných cyklů
(sluneční aktivity)
7. 104-105 let, polovina 200-letého cyklu
8. 85- 90 let
9. 78- 79 let, Gleissbergův cyklus
10. 63- 67 let, 1834-1901, (1954-?)
11. 57- 59 let
12. 51- 52 let, 1783-1834, 1901-1954
13. 43- 45 let
Přírodní jevy
Bouře na moři
Dne 11.listopadu r.1099 postihly pobřeží Anglie, Belgie a Holandska záplavy (viz např. Encyclopaedia Britannica) Záplavy se objevily v ústí řeky Temže, přičemž povodeň "vyrostla do takové výšky a napáchala tolik škody, jako si nikdo nepamatoval..." (Lowe, 1870). Při pobřežních záplavách zahynulo podle odhadů až okolo 100 000 lidí (Taylor Redd, 2012; Haigh a Bradshaw, 2015).
Dne 31.ledna r.1953 zasáhla Anglii, Belgii, Holandsko a také Skotsko velká povodeň v Severním moři (spojená s bouřkovou vlnou). Povodeň byla posouzena jako nejhorší povodeň Anglie a Skotska ve 20.století, o život přišlo několik tisíc lidí, desetitisíce zvířat a desetitisíce lidí museli opustit svůj domov. Povodeň se stala předlohou pro nizozemský katastrofický film "The storm" (2009).
Odstup těchto dvou povodní činí 1953-1099 = 854 let = 2 * 427 let. Periodu 427 letou znali již Babyloňané. Umožnovala aproximovat 36 siderických period Jupitera (36*11.862 let = 427.03 let) pomocí jeho 391 synodických period (tj. period zákrytů Slunce-Země-Jupiter, 391*398.884 dní = 427.00 let).
Nabízí se hledat, co se dělo na Zemi v r.1526 (= 1099+427 let). A skutečně: středověkou rybářskou vesnici Skegness na pobřeží Severního moře (nyní přímořské letovisko v anglickém hrabství Lincolnshire) zničila v letech 1525-26 bouře. Zajímavé může být také to, že na blízké okolí roku 1526 byla "povodeň světa" předpovídána - podle konjunkce planet - na rok 1524.
Shoda je nápadná, pobřeží Severního moře může být podle toho znovu ohroženo - v blízkém okolí roku 2380 (= 1953+427 let).
Výsledek shrneme do následující tabulky:
Holandsko r.1099 Anglie, Belgie |

Skegness r.1526 Anglie |
Holandsko r.1953 Anglie, Belgie |

Rok 2380 (predikce) Severní moře |
Erupce sopky Vesuv
V řadě let 79, 506, 933, 1360, 1787, 2214, 2641 ... s odstupem 427 let najdeme níže tři erupce sopky Vesuv, z nichž nejznámější a nejtragičtější je první z nich, z r.79:
Vesuv r.79 (zničeny Pompeje) |
Vesuv r.505 |
Vesuv r.933 |

1360? |
Vesuv r.1787 |

Rok 2214 (predikce) |
Pohyb planet
Vnější planety
Saturn v perihelu při konjunkci U-N
116-117, 618-619, 794-796, 971-972, 1472-1474, 1649-1650, 1826-1827Saturn v afelu při konjunkci U-N
278-280, 455-457, 1132-1135, 1310-1312, 1988-1989Jupiter v perihelu při konjunkci U-N
113-114, 279-280, 789-790, 800-801, 966-967, 1310-1311, 1477-1478, 1655-1656, 1821-1822, 1987-1988, 1999-2000Jupiter v afelu při konjunkci U-N
107-108, 285-286, 450-451, 628-629, 794-795, 960-961, 1139-1140, 1305-1306, 1483-1484, 1649-1650, 1815-1816, 1827-1858, 1993-1994Vnitřní planety
E-Měsíc-R-J-S
Přibližně platí: B/2 = 25∙Y = 100∙(E,R) = 225∙(E,Ln) = 18∙J, tedy
2*(E,R)/J = Y/2J = 9/25
Simulace pohybu R-J-S vytváří vzory s periodou 853.9 let.
Konjunkce Země-Mars
Konjunkce E-R se objevují poblíž geometrické osy J-S s periodou B/4. Např. (s přesností 5°) v letech 1636.3,1743.2,1850.0 či 1869.1 a 1975.9.
Platí:
([J,S]/2, Y) = 2∙B
tj. ([J,S]/2, 4∙(E,R))= (16.9132418/2, 4∙2.1353487)= (8.45662, 8.54140)=
852.04 let= 2∙426.02 let.
Osové periody vnějších planet
Předpokládejme platnost vztahů:
- synchronizace pohybu os vnějších planet s Jupiterem
([J,U],[S,N]) = 3∙J
- synchronizace pohybu os vnějších planet se slunečním cyklem
([J,N],[S,U]) = 4∙W
Z rovnic (1/J+1/U)-(1/S+1/N) = 1/(3J) a (1/J+1/N)-(1/S+1/U) = 1/(4W) plyne W= 3/4(J/2,S/3)= 11.23375 let = [J,212.1 let].
A odtud:
W= 3/4(J/2,S/3)= [J,B/2]
(Ale v porovnání s průměrnou hodnotou Slunečního cyklu W=11.0-11.1 let je hodnota 11.23 let příliš vysoká).
Odvozené periody
Perioda 71 let
Babyloňané počítali také s cyklem B/6 = 6∙J = 71.17 let (viz Zemětřesení)
65 oscilačních let dává cca 71 let, tj. 6 oběžných period Jupitera.
1.091854 let: 9/2*(E,R/2)/65 = 9/2*(0.999979,1.880711/2)/65=70.97052/65 = 9/2*15.7712270/65
- 70 let: geologický cyklus (usazeniny v jezeře Saks),
- 70 let: cyklus v letokruzích stromů (Japonský cedr)
- 70.9856 let: 65 oscilačních let, 65*(E,J)=65*1.0920855 (tropicky)
- 71.03 let: 65*1.0928, 4617/65
- 71.1391 let: 6*J (tropicky), 71.1769 let: 6*J (anomalisticky) =100 tzolkin
- 71.1785 let: B/6 = 427.07 let /6
- 71.1861 let: 4627.1/65 (925.4/13)
- 71.74 let: 2*(S,N) =2*35.87 let
- 73 let: geologický cyklus (jíl)
Perioda B/2
Extrapolace nízké sluneční aktivity z let 1800-1830 do 1980-2010 nevyšla, 180-ti letý cyklus selhal. Zde by ovšem selhal i 320-ti letý cyklus, protože v letech 1660-1690 bylo Maunderovo minimum.
Schove, Derek Justin| Schove (Šove), Derek Justin , (1913-1986), anglický meteorolog a astronom, zabýval se datováním historických událostí ve vazbě na přírodní jevy (zatmění, polární záře, povodně, bouře apod.) Autor mnoha prací, článků a knih. Zrekonstruoval zpětně hodnoty sluneční aktivity. |
V Schoveových datech se období vysoké (SSS,SS,S) a nízké (WW,W) sluneční aktivity zdají střídat spíše z periodou větší než je 180 let. Např. postupem po 205-ti letech (zhruba polovina Babylónské periody) dostáváme např. roky: 350, 555, 760, 965, 1170, 1375, 1580, 1785, 1990,…. V okolí (±40 let) těchto dat se objevují poměrně vysoká maxima. (Slapové působení planet J-V-E nemůže vytvořit takové větší rozdíly…!?).
Perioda 284 let
Simulace pohybu vnitřních planet (nad Bretagnonovými daty) potvrzují především část 2/3 z této periody, tj. periodu cca 284-287 let.
Perioda 1025 let
Možnosti fázového posunu cyklů konjunkcí J-S jsem si povšiml při čtení textů (odstavce o periodě 1020-1030 let) klimatologa Tima Niromy:
Výraznější extrémy sluneční aktivity se zdají objevovat každých cca 1025 let, tj. 6∙(U,N), 12B/5:
"Data polárních září G. L. Siscoe z let 450-1700 (Rev. Geophysics and Space Physics 18, 1980) dávají další možnost jak se pokusit vyčíslit hodnotu pro 1000-letý cyklus. Nejnižší superminimum (vyhlazené) mezi 450 a 1450 se objevilo od r.620 do r.680. Předcházelo tak nejnižší superminimum tohoto tisíciletí, Maunderovo minimum v letech 1640-1700 o 1020 let. Další superminimum po tomto pre-Maunderově je v letech 780-800, které zjevně odpovídají superminimu v letech 1800-1820 obě trváním i relativní výškou s 1020 letým odstupem. Třetí superminimum v datech Siscoe v letech 850-880 odpovídá superminimu v letech 1880-1920, o 1030 let později. Supermaxima Siscoe v letech 740-770, 820-850, a 900-930 odpovídají supermaximům začínajícím 1030, 1010, a 1050 let později, takže je poměrně zřejmý supercyklus průměrné délky 1020-1030 let."
(Timo Niroma, "Sunspots: Sunspot cycles and supercycles and their tentative causes")
Period G.L.Siscoe 1025 let: 5125/5;
minima v Eddyho diagramu Sluneční aktivity (-9625,-8600,-7575,-6550,-5525,-4500,-3475, -2450,-1425, -400, +625, 1650, 2675, 3700)
Konjunkce Uran-Neptun
Data v následující tabulce postupují zhruba s Babylonskou periodou. V levém sloupci jsou okamžiky konjunkcí E-Ln-R a okamžiky, kdy byl Jupiter v perihelu.
E-Ln-R Jp U-N --------------------------------- -2021.55 -2022.63 -1594.48 -1595.57 * (-1605.74) -1167.41 -1168.50 -740.34 -741.44 * ( -745.20) -313.26 -314.37 113.81 112.69 * ( 111.19) 540.88 539.76 967.94 966.83 * ( 965.47) 1395.01 1393.90 1822.08 1820.97 * ( 1821.01) 2249.15 2248.04 2676.22 2675.11 * ...
Možné korelace s konjunkcemi planet Uran-Neptun jsou označeny vpravo.
Kdyby byla průměrná perioda (U,N)=170.813 let, činila by 20∙ Y= 80∙ (E,R)= 240 z. Byla by v celočíselném poměru k Babylónské periodě (2:5), k 1025-ti leté periodě polárních září G.L.Siscoe (1:6) i Mayské periodě M=5125 let (1:30).
Některá s dat s periodou M/5 (tj. 5125/5 = 1025 let) se zdají nastávat
poblíž minim na Eddyho křivce sluneční aktivity:
-9625,-8600,-7575,-6550,-5525,-4500,-3475, -2450,-1425, -400, 625, 1650,
(2675), (3700).
Následující data s periodou M/3 (tj.5125/3 = 1708 let) připomínají velké
erupce sopek:
-5049 ?, -3341 Avelino, -1633 Thera, 75 Vesuv, 1783 Laki, 3491 ?.
Účinek Uranu s Neptunem
Všechna tři uvedená data bouří na moři se kryjí s okamžiky kvadratur planet Uran-Neptun. Poloha planet 31.1.1953:
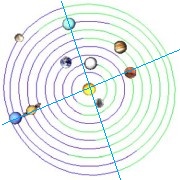
Babylónská perioda tvoří totiž poměrně přesně 2.5 násobek synodické periody Uran-Neptun: 427 let = 2.5 * 170.8 let.
Také erupce v okolí roku 1787 (tj.výbuch Etny r.1787, Stromboli 1783, Laki r.1783-84) nastaly poblíž kvadratury planet Uran-Neptun. Poloha planet 1.7.1787:
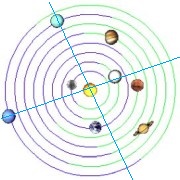
Velká nerovnost
Velká nerovnost (J/2,S/5) činí cca 2∙B=400∙(E,R). Předpokládejme, že I=
2∙B = 72∙J = 29∙S' = 43∙(J,S').
Pak použitím J=11.8620 dostáváme: I=854.06 let, B=427.03 let, S' =
29.450441 let. Synodická perioda (J,S') = 19.861925 let.
Kdyby měla velká nerovnost J-S hodnotu právě I= 2∙B= 854.06 let, pak by
se odvozené periody lišily od Bretagnonových poměrem:
S/S'=29.457158/29.450441 =1.000228; resp.
(J,S')/(J,S)=19.861925/19.8588709= 1.000154.
Laplaceův cyklus
7*61 let = 427 let, odtud 854 let vs.Laplaceův cyklus. Datování:
... 59, 273 - 486, 700, 913, 1127 - 1340, 1554, 1767, 1981 - 2194, 2408, 2621,...
- r.1340 uprostřed období zesílení (vysoká aktivita)-střední rychlost Jupitera,
- r.1553-1554 je uprostřed přechodného období (nízká aktivita) - vyšší rychlost Jupitera,
- r.1760 - střední rychlost Jupitera,
- r.1981 je uprostřed přechodného období (nízká aktivita) - nižší rychlost Jupitera,
Překrývání cyklů
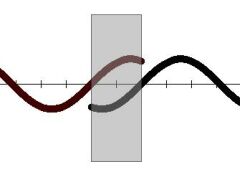 Odlehlost konjunkcí
Odlehlost konjunkcí
Synodická perioda je průměrná perioda opakování konjunkcí. Ve skutečnosti konjunkce (v důsledku eliptických drah a nerovnoměrného pohybu těles) nastávají v proměnlivých intervalech.
Např. konjunkce J-S, v letech 1940-2000: r.1940.85, (20.41), r. 1961.26, (20.01), r.1981.28, (19.15) a r.2000.43 (v závorce jsou intervaly).
Konjunkce J-S
Intervaly konjunkcí Jupitera se Saturnem se opakují po trojicích, tj. s průměrnou periodou cca 60 let (Čínský astrologický cyklus), 3∙(J,S) = 3∙19.859 = 59.577 let .
Každých cca 900 let (velká nerovnost) dojde k fázovému posunu a nastoupí nová posloupnost trojic.
Např. maximální odstup cca 20.5 let se objevuje před konjunkcemi r. 750.03, r.1723.11 a r.2636.65.
I. r. 750.03
0: ( 20.49) 750.03 ( 19.59) 769.62 ( 19.47) 789.08 1: ( 20.48) 809.56 ( 19.69) 829.25 ( 19.38) 848.63 2: ( 20.48) 869.11 ( 19.77) 888.88 ( 19.32) 908.20 3: ( 20.45) 928.65 ( 19.86) 948.51 ( 19.25) 967.76 4: ( 20.42) 988.18 ( 19.96) 1008.14 ( 19.19) 1027.34 5: ( 20.38) 1047.72 ( 20.04) 1067.76 ( 19.15) 1086.91 6: ( 20.34) 1107.26 ( 20.11) 1127.37 ( 19.14) 1146.50 7: ( 20.29) 1166.79 ( 20.18) 1186.97 ( 19.12) 1206.09 8: ( 20.22) 1226.31 ( 20.26) 1246.57 ( 19.12) 1265.70 9: ( 20.15) 1285.85 ( 20.31) 1306.16 ( 19.15) 1325.32 10: ( 20.07) 1345.39 ( 20.36) 1365.74 ( 19.19) 1384.93 11: ( 19.97) 1404.91 ( 20.41) 1425.32 ( 19.25) 1444.57 12: ( 19.88) 1464.44 ( 20.45) 1484.90 ( 19.30) 1504.20 13: ( 19.78) 1523.98 ( 20.48) 1544.46 ( 19.37) 1563.83 14: ( 19.70) 1583.53 ( 20.48) 1604.01 ( 19.47) 1623.47 15: ( 19.59) 1643.06 ( 20.49) 1663.56 ( 19.55) 1683.11
II. r. 1723.11
0: ( 19.51) 1702.61 ( 20.49) 1723.11 ( 19.64) 1742.75 1: ( 19.41) 1762.16 ( 20.49) 1782.66 ( 19.73) 1802.38 2: ( 19.34) 1821.73 ( 20.47) 1842.19 ( 19.84) 1862.03 3: ( 19.26) 1881.29 ( 20.44) 1901.73 ( 19.92) 1921.65 4: ( 19.21) 1940.85 ( 20.41) 1961.26 ( 20.01) 1981.28 5: ( 19.15) 2000.43 ( 20.37) 2020.80 ( 20.08) 2040.88 6: ( 19.14) 2060.02 ( 20.31) 2080.34 ( 20.16) 2100.50 7: ( 19.11) 2119.61 ( 20.25) 2139.86 ( 20.23) 2160.09 8: ( 19.12) 2179.22 ( 20.18) 2199.39 ( 20.30) 2219.70 9: ( 19.12) 2238.82 ( 20.11) 2258.93 ( 20.34) 2279.27 10: ( 19.16) 2298.44 ( 20.01) 2318.45 ( 20.40) 2338.85 11: ( 19.22) 2358.07 ( 19.92) 2377.99 ( 20.44) 2398.43 12: ( 19.27) 2417.70 ( 19.82) 2437.52 ( 20.47) 2457.99 13: ( 19.34) 2477.33 ( 19.73) 2497.06 ( 20.49) 2517.55 14: ( 19.43) 2536.98 ( 19.63) 2556.61 ( 20.49) 2577.10
III. r. 2636.65
0: ( 19.51) 2596.61 ( 19.53) 2616.15 ( 20.51) 2636.65 1: ( 19.60) 2656.26 ( 19.45) 2675.71 ( 20.49) 2696.20 ....
Nový cyklus je vždy posunut oproti předchozímu ve fázi o průměrně
(J,S)=19.859 let.
Fázové posuvy způsobují, že se průměrný cyklus konjunkcí (vzhledem k
intervalům odlehlosti) jeví (statisticky,...) nepatrně delší, přibližně
19.859∙(n+1)/n, kde n je cca 42-48.
Trojice pak trvá cca 61 let, tj. přibližně (J,S/2)=60.95 let (1/7
Babylonské periody 427 let).
| Spörer Gustav , 1822-1895, amatérský astronom, nezávisle na R.Ch.Carringtonovi objevil časovou závislost výskytu skvrn na vzdálenosti od rovníku - ‘motýlkový diagram’ a vyslovil domněnku, že Sluneční aktivita před r.1716 byla velmi slabá. |
Dlouhodobé změny
Největší odchylky od průměrných konjunkčních intervalů planet Jupiter a Saturn jsou působeny:
· planetami Jupiter a Saturn samými (eliptické dráhy, velká nerovnost)
· planetami Uran a Neptun (perturbace).
Průměrnými cykly těchto změn jsou:
· cyklus 60-61 letý (59.58 let, s fázovým posunem, viz výše)
· cyklus 85.5 letý (85.72 let = (U,N)/2 = 171.44/2 let)
Pokusme se tyto dva cykly složit.
S ohledem na fázové posuny napíšeme funkci pro každý interval (cca
800-1000 let).
Přesné okamžiky posuvů nejsou jasné - snad ani neexistují - jeden z cyklů
zaniká zatímco jiný sílí.
Interval Funkce ----------------------------------------------------------------- (-2000,-1000) |Ap∙sin(2π(t-1111)/P)+Aq∙sin(2π(t-1157)/Q)| (-1000, 0) |Ap∙sin(2π(t-1131)/P)+Aq∙sin(2π(t-1157)/Q)| ( 0, 1000) |Ap∙sin(2π(t-1151)/P)+Aq∙sin(2π(t-1157)/Q)| ( 1000, 2000) |Ap∙sin(2π(t-1171)/P)+Aq∙sin(2π(t-1157)/Q)| ( 2000, ... ) |Ap∙sin(2π(t-1191)/P)+Aq∙sin(2π(t-1157)/Q)| ....
Zde P=3∙(J,S)=59.58 let, Q=(U,N)/2=85.72 let, Ap,Aq
nějaké konstanty a t čas [let]. V hodnotách r.1111, r.1131, r.1151,
r.1171 jsou patrné cca 20-ti leté fázové posuny.
Hodnota 1157 byla zvolena 20 let po konjunkci (U,N).
Egyptské minimum (-1300,-1200), Homérovo minimum (-800,-700)
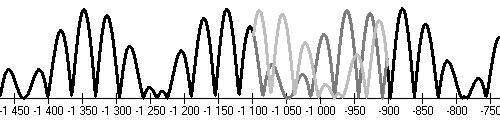
Řecké minimum (-450,-350)
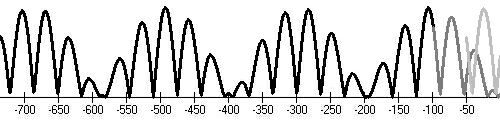
|
Středověké minimum (650,705)

Středověké maximum (1120,1280), Wolfovo minimum (1280,1340)
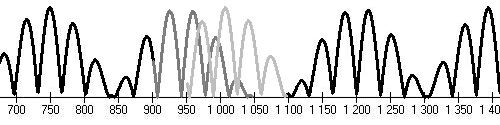
| Maunder, Edward Walter , 1851-1928, Anglický astronom, zabýval se spektroskopií, fotografováním slunečních skvrn, pozorováním komet, Marsu apod. Potvrdil Spörerovu domněnku, že Sluneční aktivita před r.1716 byla velmi slabá. |
Sporerovo minimum (1400,1500), Maunderovo minimum (1645,1715), minimum
(1870,1930), maximum konce tisíciletí (1930-2030)
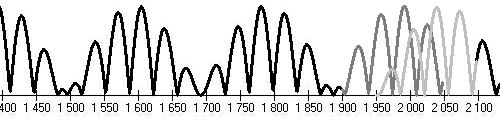
Poznámky:
- Maunderovo minimum začalo okolo r.1650. Analogický "nulový bod" byl např. v r. 800, t.j. o 850 let (2∙B, t.j. 12 Brucknerových cyklů) před Maunderovým.
- Porovnání s maximy podle J.Šove:
175-200, (290-300?), 350-375, 500-510, 530, 565, 585, (675?), 745,765,
(830-840?), 920-930, 960-980, (1100-1150), (1200), 1360-1370,
1530-1580, 1720-1740, 1770-1790,(1840-1870?), 1940-1990,...
| Eddy, John A. , 1931-2009, Americký astronom, sbíral data z nejrůznějších zdrojů a zrekonstruoval zpětně hodnoty sluneční aktivity. Upřesnil období tzv.Maunderova minima (1645-1715) a definoval tzv.Spörerovo minimum (1460-1550). |
-
Diagramy nevysvětlují minimum v letech 1800-1820.
Okolo r. 1820 nastala zároveň konjunkce J-S (1821.76), U-N (1821.01) (a smyčka barycentra); J byl v perihelu (1821.37). - G.Sporer upozornil na možnost nízké aktivity v letech 1887-1889.
Jiná data:
| Minima | Maxima |
|
m2-1: 1040 m2-2: 1160 m2-3: 1270-1330 m2-4: 1410-1500 m2-5: 1670 m2-6: 1820 m2-7: 1880 |
M2-1: 1130 (1100-1150) M2-2: 1190 (1170-1220) M2-3: 1370 M2-4: 1610 M2-5: 1720-1780 M2-6: 1860 M2-7: 1960? |
Synchronizace odchylek
Oba uvedené cykly se setkávají cca po uplynutí Babylonské periody 427 let: 61.0 ∙7 = 427.0 let, 85.5 ∙5 = 427.5 let.
Odvozené periody:
- [(J,S/2), (U,N)/2]= [60.95, 85.72]= 35.6 let (Brucknerova perioda),
- ((J,S/2), (U,N)/2)= (60.95, 85.72)= 210.9 let (polovina Babylónské periody).
Jsou tyto cykly synchronizovány? Předpokládejme, že platí:
P=a1∙P1+F1 = a2∙P2+F2, kde a1=14, P1=59.577 let, F1=19.859 let a a2=5,
P2= 171.44 let, F2=?
Pak P = 14∙59.577 + 1∙19.859 = 43∙19.859 = 853.94 let (2∙B) a fázový
posun F2 = P- 5∙171.44 = -3.27 let.
Kdyby bylo F2= 0, pak (U,N) = 2∙B/5 = 2∙36∙J/5 = 427.031/5=170.813
let.
A odtud zpětně Neptunova perioda: N = ((U,N),U)= (170.813, 84.020)=
165.358 let. (Odchylka 0.4 % od Bretagnonovy střední periody 164.770
let).
Předpověď
Pro roky 2000-2700.
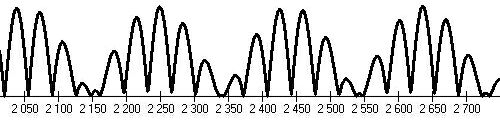
V období okolo r. 2150, r.2350 a r. 2500 by mohla být další "Maunderova minima"..?.