Schematická algebra - Segmentace
Segmenty systémů
Vnořování (viz Vnořování G-systémů) je záležitostí G-systémů s
konstantním n.
Nyní budeme vyšetřovat G-systémy s konstantním k.
G(2,2) => G(3,2)
0 0
1 2 1 3
3 4
6 2
7 5
8
Vyčlenění segmentů
Každý G-systém můžeme rozdělit na segmenty tak, že oddělíme nové instance od instancí, které G-systém získal od systémů s nižším n.
Např. systém G(3,2) je rozšířením systému G(2,2):
Každý G(n,k) má n druhů vnořených z G(n,1). Uvažujme, že tyto druhy rozdělují G-systém do segmentů. V segmentu s (s<n) má každý takový druh číslo
g(s) = (n−s) ∙ (nk−1) / (n−1)
Jestliže nějaký segment existuje v G(n,k), pak podobný segment existuje také v G(n+1,k). Tato věta se objasní přepíšeme-li základní schema instancí na schema kontrastní (viz Typy schemat). Všechna čísla u nahradíme čísly u'=r−u = (nk−1)−u. Přitom segmenty přečíslujeme na s'=(n−s).
Např. segmenty v G(3,3):
u:
|
u':
0 segment 0'
──────────────────
9 1 3
12 10 4
13
segment 1'
──────────────────
18 2 6
19 5 15
21 11 7
22 14 16
24 20 8
25 23 17
26
segment 2'
|
Číselné soustavy
Čísla nk−1−u z předchozí tabulky vyjádříme jako funkce n:
k=2 k=3
segment 0 segment 0
1 1
segment 1 segment 1
n 1 n2 1 n
n+1 n2+n n2+1 n +1
n2+n+1
A zapíšeme koeficienty těchto funkcí (polynomů):
k=2 k=3
segment 0 segment 0
0 0 0 0 0
segment 1 segment 1
1 0 0 1 1 0 0 0 0 1 0 1 0
1 1 1 1 0 1 0 1 0 1 1
1 1 1
Každý G-systém je množinou čísel z n-kové číselné soustavy.
| G-relace rozděluje G(n,k) do n segmentů, kde každý segment s užívá právě s symbolů, s=0..n−1. |
Součet koeficientů polynomů je stejný pro všechny instance daného druhu (instance téhož druhu mají stejnou úroveň).
Skladba G-systémů
Příklad G(n,2)
G(1,2) 00 00 00
─────────────────────────
10 01 10 01 10 01
G(2,2) 11 11 11
─────────────────────────
20 02 20 02 20 02
21 12 21 12 21 12
G(3,2) 22 22 22
─────────────────────────
30 03 30 03
31 13 31 13
32 23 32 23
G(4,2) 33 33
─────────────────────────
40 04
41 14
42 24
43 34
G(5,2) 44
|
Příklad G(n,3)
G(1,3) 000 000 000
────────────────────────────────────────────
100 001 010 100 001 010 100 001 010
110 101 011 110 101 011 110 101 011
G(2,3) 111 111 111
────────────────────────────────────────────
200 002 020 200 002 020
201 012 120 201 012 120
210 102 021 210 102 021
211 112 121 211 112 121
220 202 022 220 202 022
221 212 122 221 212 122
G(3,3) 222 222
────────────────────────────────────────────
300 003 030
301 013 031
302 023 032
310 103 130
311 113 131
312 123 132
320 203 230
321 213 231
322 223 232
330 303 330
331 313 331
332 323 332
G(4,3) 333
|
Elektronové podslupky v atomech
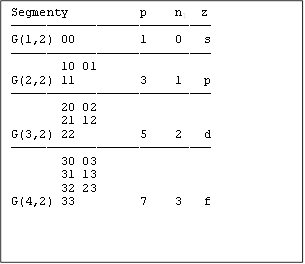
Počet elekronů p v podslupce s vedlejším kvantovým číslem nl odpovídá počtu instancí v nl−tém segmentu G-systémů řádu k=2.
(Ve sloupci z je užívané označení podslupek).
Vlastní druhy
Počet vlastních druhů v segmentech se získá jako rozdíl počtu vlastních druhů ze dvou systémů, jejichž základy se liší o jedničku, tj:
s(n,k) = v(n+1,k)−v(n,k)
Počty vlastních druhů v segmentechPočty vlastních druhů v segmentech s(n,k) zapsané funkcemi proměnné n:
k m(n,k) ──────────────────────────── 1 1 2 n 3 n∙(n+1) 4 (n/2)∙(2n²+3n+1) 5 n∙(n³+2n²+2n+1) 6 (n/6)∙(6n4+15n³+20n²+12n+1) 7 n∙(n5+3n4+5n³+5n²+3n+1) 8 (n/4)∙(4n6+14n5+28n4+35n³+26n²+11n+4) |
0 1 2 3 4 5 6 7 ───────────────────────────────────────── 1 1 1 1 1 1 1 1 0 1 2 3 4 5 6 7 0 2 6 12 20 30 42 56 0 3 15 42 90 165 270 423 0 6 42 156 420 930 1806 3192 0 9 107 554 1910 5155 11809 24052 0 18 294 2028 8820 28830 77658 181944 0 30 780 7350 40590 161040 510510 1376340 |
Způsob výpočtu s(n,4) je známý z matematických hříček: 3= 1+2; 15= 4+5+6; 42= 9+10+11+12; 90= 16+17+18+19+20.
Druhy celkem
Obdobně jako v předchozím odstavci:
t(n,k) = m(n+1,k)−m(n,k)
Počty druhů v segmentechPočty všech druhů v segmentech t(n,k) zapsané funkcemi proměnné n:
k t(n,k) ───────────── 1 1 2 n+1 3 n²+n+1 |
0 1 2 3 4 5 6 7 ───────────────────────────────── 1 1 1 1 1 1 1 1 1 2 3 4 5 6 7 8 1 3 7 13 21 31 43 57 |
Instance celkem
Obdobně je také:
S(n,k) = M(n+1,k)−M(n,k) = (n+1)k−nk
Kronecker Leopold| Kronecker Leopold , [] 1823-1891, německý učenec a matematik spojovaný s ideou aritmetizace matematiky, oponent Cantorových koncepcí. Zabýval se aritmetikou kvadratických forem, teorií ideálů a eliptickými funkcemi. Odmítl aktuální nekonečno. Veškerá matematika má být založena na číslech a všechna čísla na přirozených číslech: "Přirozená čísla jsou od Boha, ostatní je dílem člověka." |
Počty všech instancí v segmentech S(n,k) zapsané funkcemi proměnné n:
k S(n,k) ───────────────── 1 1 2 2n+1 3 3n²+3n+1 4 4n³+6n²+4n+1 |
0 1 2 3 4 5 6 7 ───────────────────────────────────── 1 1 1 1 1 1 1 1 1 3 5 7 9 11 13 15 1 7 19 37 61 91 127 169 .... |
Počet S(n,k) – nazývaný tak - Kroneckerovo delta - má vztah k Bernouliho posloupnostem (viz Trojúhelníky) a k otázce velké Fermatovy věty.
Periodické posloupnosti
Perioda posloupnosti
Mějme posloupnost čísel an. Pokud existuje takové číslo r, že pro všechna n platí an+r = an, tak říkáme, že {an} je periodická posloupnost. Číslo r se nazývá perioda posloupnosti. Nejmenší z period dané posloupnosti je základní (přirozená) perioda .
Členy rozdílových posloupností
Obecně r-tý člen s-té rozdílové posloupnosti
|
as,r = ∑(−1)i ∙
|
(sčítáme pro i=0..s) :
V posloupnosti třetích mocnin je:
s\r 1 2 3 4 5 6 ... ──────────────────────────── 0 0, 1, 8,27,64,125,... 1 1, 7,19,37,61,... 2 6,12,18,24,... 3 6, 6, 6,...
Pro i=0,..,2:
a2,3 = ∑(-1)i a3+2-i =
![]() a5 -
a5 -
![]() a4 +
a4 +
![]() a3
= a5- 2a4 +a3 = 64 - 2*27 + 8 = 18
a3
= a5- 2a4 +a3 = 64 - 2*27 + 8 = 18
V posloupnosti řádu s je s-tá rozdílová posloupnost konstantní, tj.
každý člen této rozdílové posloupnosti je roven 0-tému členu:
as,0 = ∑(−1)i
![]() as−i = Ks .
as−i = Ks .
V případě Kp= p! = 0 mod p (pεP) analogicky platí:
ai+p + (−1)p ai = 0 mod p
Například pro p-té mocniny: (i + p)p + (−1)p ∙ ip = 0 mod p.
Pro p = 2: a0 = 0; a1 = 1; a2 = 4;
a3 = 9; a4 = 16; a5 = 25;
a2+a0= 4, a3+a1 = 10 is 0 mod
2.
Pro p = 3: a0 = 0; a1 = 1; a2 = 8;
a3 = 27; a4 = 64; a5 = 125;
a3−a0= 27, a4−a1 = 63 is 0
mod 3.
Když pεP, tak platí Wilsonova věta: K(p)=(p−1)! ≡ −1 (mod p). Pro každé i = 1..p−1 je
![]() = 0 mod p.
= 0 mod p.
V součtu zbývá proto jen první a poslední člen: a(p) + (−1)p ∙ a0 = −1 (mod p)
Protože všechny členy p-té rozdílové posloupnosti se rovnají, můžeme vybrat jiný člen, i-tý (místo 0-tého):
a(i+p) + (−1)p ∙ ai = −1 (mod p)
Přirozená perioda
Nechť qεQ má prvočíselný rozklad: q = součin(pjaj), pjεP, ajεZ. Přirozenou periodou R nazýváme číslo: R = ∏pj.
n\k 1 2 3 4 5 6 7 8 9 10 11 12 ─────────────────────────────────────── 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 2 0 0 2 0 2 4 2 0 8 4 2 4 3 0 1 0 1 3 3 3 1 0 9 3 9 4 0 0 1 0 4 4 4 0 1 6 4 4 5 0 1 2 1 0 1 5 1 8 5 5 1 6 0 0 0 0 1 0 6 0 0 6 6 0 7 0 1 1 1 2 1 0 1 1 9 7 1 8 0 0 2 0 3 4 1 0 8 4 8 4 9 0 1 0 1 4 3 2 1 0 1 9 9 10 0 0 1 0 0 4 3 0 1 0 10 4 11 0 1 2 1 1 1 4 1 8 1 0 1 12 0 0 0 0 2 0 5 0 0 4 1 0 ─────────────────────────────────────── R 1 2 3 2 5 6 7 2 3 10 11 6
Počet zbytkových tříd výrazu nk mod k, n,kεN0, je roven přirozené periodě R čísla k.
Přirozené druhy
Přirozené druhy V G-systémech
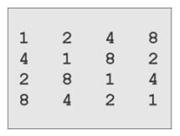
Instance každého druhu G-systému seřadíme do vzestupné posloupnosti. Jestliže všechny rozdíly instancí {d1,d2,...} jsou tvaru B∙(nj), j=0..k−1,
říkáme, že jde o přirozený druh (N-druh).
Rozdíly {d1,d2,...} v G(n,k) jsou vždy dělitelné
n−1.
Rozdíly instancí
Konstrukce přirozených druhů v G(2,4)Instance Přeřazení Rozdíly Typ Nb ──────────────────────────────────────────────────────── 0 0 x − 1 2 4 8 1 2 4 8 1 2 4 N1 3 6 12 9 3 6 9 12 3 3 3 − 5 10 => 5 10 => 5 − 7 14 13 11 7 11 13 14 4 2 1 N1 15 15 x −
Instance Rozdíly Typ Nb ──────────────────────────────────────────────────────── 0 − − 1 2 4 8 16 1 2 4 8 N1 5 9 10 18 20 => 4 1 8 2 N1 11 13 21 22 26 2 8 1 4 N1 15 23 27 29 30 8 4 2 1 N1 31
Typ přirozeného druhu označíme Nb, kde b = B/(n−1). Pro n=2 je B=b=1 (dosavadní příklady); pro n=3, je B=2,4 a b=1,2; pro n=4, je B=3,6,9 a b=1,2,3; atd.
Výpisy
G(2,2): x G(3,2): x G(4,2): x
1 P 2 P 3 P
x 4 P 6 P
k=2; φ(2) = 1 x 9 P
2 P x
x 3 P
6 P
x
3 P
x
G(2,3): G(3,3): G(4,3):
x x x x
1 2 P 2 6 P 3 12 P 3 12 P
2 1 P 4 12 P 6 24 P 6 24 P
x 6 2 P 9 36 P 12 3 P
10 4 12 3 P 18 9
4 10 18 9 9 18
k=3; φ(3) = 2 12 4 P 21 21 24 6 P
x 9 18 x
2 6 P 24 6 P 3 12 P
6 2 P 33 6 12 3 P
x 6 33 x
21 21
36 9 P
G(2,4): G(3,4):
x x 40
1 2 4 P 2 6 18 P 12 4 28
3 3 3 4 12 36 P 24 14 8
5 8 16 8 10 30 10
4 2 1 P 10 30 10 36 12 4 P
x 14 8 34 x
16 32 16 2 6 18 P
k=4; φ(4) = 2 20 8 16 8
8 14 24 20
18 6 2 P 18 6 2 P
28 4 12 x
16 16 16
34 8 14
Sepsáním diferencí přirozených druhů za sebe dostáváme některé latinské čtverce a podobné obrazce:
k=2: 1 k=3: 1 2 k=4: 1 2 4 k=5: 1 2 4 8
2 1 4 2 1 4 1 8 2
2 8 1 4
8 4 2 1
k=6: k=7: k=8:
1 2 4 8 16 1 2 4 8 16 32 1 2 4 8 16 32 64
16 8 4 2 1 8 1 16 2 32 4 4 32 1 8 64 2 16
16 4 1 32 8 2 16 2 64 8 1 32 4
2 8 32 1 4 16 64 32 16 8 4 2 1
4 32 2 16 1 8
32 16 8 4 2 1
Identifikace druhů
Pro čísla N-druhů g(j) v G(n,k) platí:
(nj−1)∙g(j) mod (nk−1) = b∙(n−1)∙nj−1
kde nsd(j, k) = 1.
Symbol b označuje číslo typu N-druhu, b=1..s.
Pro jakýkoliv N-druh g ze segmentu s systému G(n,k) existuje:
kontrastní N-druh g'; g+g'=nk-1. odpovídající N-druh g' v G(n+1,k) (vnořování) odpovídající N-druh g' v segmentu s+1 (segmentace)Instances Differences Type Nb ──────────────────────────────── 0 - - 1 3 9 2 6 N1 2 6 18 4 12 N2 4 12 10 6 2 N1 5 15 19 10 4 - 7 21 11 4 10 - 8 24 20 12 4 N2 13 - - 14 16 22 2 6 N1 17 25 23 6 2 N1 26
Pro číslo typu N-druhu b=1, není příslušné g-číslo soudělné s
nk−1.
Např. v systému G(2,4) druhy g=1 a g=7 nejsou soudělné s 15.
Počet druhů v G-systémech
Každý segment s má N-druhy s číslem typu b=1..s.
Přitom v G(n,k) existuje (n−b) ∙ φ(k) N-druhů g(j) s číslem typu b.
Dohromady je to s∙φ(k) N-druhů (t.j. k∙s∙φ(k) N-instancí).
Celkový počet N-druhů v G(n,k) je: n−1 n−1 n ∑(s∙φ(k))=φ(k) ∑(s)=φ(k) ∑(n−b)=φ(k)∙n∙(n−1)/2 N−druhů s=0 s=0 b=1
(Koeficient n(n−1)/2 připomíná počet vazeb mezi n prvky).
Systém G(3,3) má φ(3)∙3(3−1)/2=6 přirozených druhů (s číslem typu b=1 nebo b=2):
Počet druhů v binárních G-systémech
V G(2,k) existuje φ(k) N-druhů g(j). (2j−1)∙g(j) mod (2k−1) = 2j−1 pro nsd(j, k) = 1.
Součet hodnot g(j) (j=1..φ(k)) je: ∑(g) = 2k−2 ∙ φ(k)
Např. pro G(2,4) dostáváme:
Instance Type Nb ────────────────────────── 0 − 1 2 4 8 N1 (j=1) 3 6 12 9 − 5 10 − 7 14 13 11 N1 (j=2) 15 − |
Řešení: (mod 15)
j = 1: 1∙g ≡ 1 g = 1
j = 2: 3∙g ≡ 2 g = 11
|
Součet: 1+7= 8= 24−2 ∙ φ(4).
Pro G(2,5) platí:
Instance Typ Nb ─────────────────────────────── 0 − 1 2 4 8 16 N1 (j=1) 5 9 10 18 20 N1 (j=3) 11 13 21 22 26 N1 (j=2) 15 23 27 29 30 N1 (j=4) 31 − |
Řešení: (mod 31) j = 1: 1g ≡ 1 g = 1 j = 2: 3g ≡ 2 g = 11 j = 3: 7g ≡ 4 g = 5 j = 4: 15g ≡ 8 g = 15 |
Součet 1+11+5+15 = 32 = 25−2 ∙ φ(5).
Podobně pro k = 7 (mod 127): j= 1: 1∙g ≡ 1 g= 1 j= 4: 15∙g ≡ 8 g= 9 j= 2: 3∙g ≡ 2 g= 43 j= 5: 31∙g ≡ 16 g= 21 j= 3: 7∙g ≡ 4 g= 55 j= 6: 63∙g ≡ 32 g= 63
Součet: 1+43+55+9+21+63 = 192 = 27−2 ∙ φ(7)
Přirozené druhy v M-systémech
Pro přirozené druhy (N-druhy) g(j) platí:
(nj−1)∙g(j) mod r = b∙nj−1
pro nsd(j, k) = 1.
M(3,3) má všechny vlastní druhy přirozené, r = ( 33-1)/(3-1) = 26/2 = 13:
Instance Rozdíly Typ Nb
─────────────────────────────
0 - -
1 3 9 2 6 N2
2 6 5 3 1 N1
4 12 10 6 2 N2
7 8 11 1 3 N1
13 - -
M(3,4) má jen 2 přirozené druhy, r = ( 34−1)/(3−1) = 80/2 = 40:
Instances Differences Type Nb
────────────────────────────────────
0 − −
1 3 9 27 2 6 18 N2(j=1)
2 6 18 14 4 8 4 −
4 12 36 28 8 16 8 −
5 15 10 −
7 21 23 29 14 2 6 −
8 24 32 16 8 8 8 −
10 30 20 −
11 33 19 17 6 2 14 −
13 39 37 31 18 6 2 N2(j=3)
20 − −
22 26 38 34 4 8 4 −
25 35 10 −
40 − −
|
b = 1: (mod 40)
j=1: (31−1)∙ g≡ 1 nemá řešení
j=2: (3²−1)∙ g≡ 3 nemá řešení
j=3: (3³−1)∙ g≡ 9 nemá řešení
b = 2: (mod 40)
j=1: (31−1)∙ g≡ 2∙1 g = 1
j=2: (3²−1)∙ g≡ 2∙3 nemá řešení
j=3: (3³−1)∙ g≡ 2∙9 g = 13
|
V M(3,5), r = (35−1)/(3−1) = 242/2 = 121 existují pro b = 1 přirozené druhy:
Instance Typ Nb ──────────────────────────── 0 − 1 3 9 27 81 − 2 6 18 54 41 − 4 12 36 108 82 − * 5 15 45 14 42 N1(j=3) 7 21 63 68 83 − 8 24 72 95 43 − 10 30 90 28 84 − 11 33 99 55 44 − 13 39 117 109 85 − 16 48 23 69 86 − 17 51 32 96 46 − 19 57 50 29 87 − * 20 60 59 56 47 N1(j=4) 22 66 77 110 88 − 25 75 104 70 89 − 26 78 113 97 49 − 31 93 37 111 91 − 34 102 64 71 92 − 35 105 73 98 52 − 38 114 100 58 53 − 40 120 118 112 94 − * 61 62 65 74 101 N1(j=1) 67 80 119 115 103 − * 76 107 79 116 106 N1(j=2) 121 − |
b = 1: (mod 121)
j= 1: (31−1)∙ g ≡ 1 g = 61
j= 2: (3²−1)∙ g ≡ 3 g = 76
j= 3: (3³−1)∙ g ≡ 9 g = 5
j= 4: (34−1)∙ g ≡ 27 g = 20
|
Prvočísla v R−systémech
Prvočíselná věta
Počet prvočísel menších než dané číslo r se značí π(r). Z prvních
Eulerových a Legendreových odhadů vyplynulo, že hodnota π(r) roste
přibližně stejně rychle jako funkce r/ln(r).
Kompletní důkaz, že (v limitě do nekonečna) platí π(r) ~ r/ln(r),
předvedli metodami komplexní analýzy J.Hadamard a Vallée−Poussin. Hodnoty
π(r) jsou tabulovány,viz např.[Narkiewicz]:
| Hadamard, Jacques , 1865-1963, francouzský matematik, dokázal (r.1896) prvočíselnou větu. |
π(10²) = 25
π(10³) = 168
...
π(109) = 50847534
| Vallée-Poussin, Charles-Jean de la , 1866-1962, belgický matematik, dokázal (r.1896) - nezávisle na Hadamardovi - prvočíselnou větu. |
…
...
π(1018) = 24739954287740860
π(1019) = 234057667276344607
π(1020) = 2220819602560918840
...
| Riemann, Georg Friedrich Bernhard , 1826-1866, německý matematik, známý svým systémem neeuklidovské geometrie. Do teorie čísel zavedl (r.1859) tzv.zeta funkci a formuloval tzv.Riemannovu hypotézu o rozložení prvočísel. |
O lepší aproximaci počtu prvočísel se pokusil G.Riemann.
P.L.Čebyšev (r.1852) dokázal
tzv. slabou formu prvočíselné věty.
Z této plyne např. že v celém intervalu rε N se r/ln(r) neodchyluje
nikde od π(r) o více než 11% [Zelinka].
Bez použití komplexní analýzy dokázal prvočíselnou větu (r.1949)
A.Selberg.
| Dirichlet, Peter Lejeune [Dirichle], 1805-1859, německý matematik. Zabýval se teorií čísel, dokázal platnost velké Fermatovy věty pro exponent k=5. Do variačního počtu zavedl nový princip. v teorii čísel používal analytických funkcí. Dokázal konvergenci Fourierových řad. |
Dirichlet dokázal, že každá aritmetická posloupnost 1. řádu (a,a+d,a+2d,...) s charakteristikou [d,a] tvořenou nesoudělnými čísly (a,d)=1, obsahuje nekonečný počet prvočísel.
Prvočísla v G-systémech
Zajímá nás, jestli struktura G-systému nemá nějaký vliv na
rozložení prvočísel. Instance druhů nesoudělných s modulem r budou
zahrnovat všechna prvočísla, která nenajdeme v prvočíselném rozkladu
modulu r.
Např. v G(3,3) je φ(26)=12 instancí nesoudělných s 26:
Protože 26 = 2*13, musí být všechna prvočísla menší než 26, kromě 2 a 13, mezi těmito 12-ti instancemi: 1, 3, 5, 6, 7, 9, 15, 17, 19, 21, 23, 25. To jsou: 3,5,7,17,19 a 23.
0 1 3 9 2 6 18 4 12 10 5 15 19 7 21 11 8 24 20 13 14 16 22 17 25 23 26
R(17,12,210)
0
1 17 79 83 151 47 169 143 121 167 109 173
2 34 158 166 92 94 128 76 32 124 8 136
3 51 27 39 33 141 87 9 153 81 117 99
4 68 106 122 184 188 46 152 64 38 16 62
5 85 185 205 125 25
6 102 54 78 66 72 174 18 96 162 24 198
7 119 133 161
10 170 160 200 40 50
11 187 29 73 191 97 179 103 71 157 149 13
12 204 108 156 132 144 138 36 192 114 48 186
14 28 56 112
15 45 135 195 165 75
19 113 31 107 139 53 61 197 199 23 181 137
20 130 110 190 80 100
21 147 189 63
22 164 58 146 172 194 148 206 142 104 88 26
30 90 60 180 120 150
35 175
37 209 193 131 127 59 163 41 67 89 43 101
42 84 168 126
44 118 116 82 134 178 86 202 74 208 176 52
49 203 91 77
55 95 145 155 115 65
57 129 93 111 207 159 183 171 177 69 123 201
70 140
98 196 182 154
105
210
Úroveň: 1 2 3 4 5 6 7 8 9 10 11 12 * Celkem ────────────────────────────────────────────────────────────────── Tříd: 3 2 0 6 0 6 0 0 0 0 0 12 * 29 Instancí: 3 4 0 24 0 36 0 0 0 0 0 144 * 211
Čísla n s vyšším poměrem n/φ(n):
n φ(n) n/φ(n) ──────────────────── 210 48 4,38 330 80 4,13 390 96 4,06 420 96 4,38 630 144 4,38 660 160 4,13 780 192 4,06 840 192 4,38 990 240 4,13 1050 240 4,38 1170 288 4,06 1260 288 4,38
Součty mocnin instancí
Součtování v G-systémech
Vyčísleme součet čísel instancí ve všech druzích G(3,3):
0 0
1 3 9 13
2 6 18 26
4 12 10 26
5 15 19 39
7 21 11 39
8 24 20 52
13 13
14 16 22 52
17 25 23 65
26 26
Každý součet je dělitelný číslem M(n,k)=(nk−1)/(n−1) = (3³−1)/(3−1) = 13.
V G(n,k), platí pro každý druh gi (v součtu přes j):
∑ ui (j) = 0 ( mod M(n,k))
Výpočet součtu
Platí (v součtu přes j):
∑ ui (j) = L(gi) ∙ c(k,q) ∙ q/k)
kde q je počet transpozic (tj.řád výchozího vnořeného systému), L(gi) úroveň druhu gi a c(k,q) koeficient vnoření.
Např. v G(3,3) platí:
L(7) ∙c(3,1) ∙ 3/3 = 3∙ ((33−1)/(3−1))∙1 = 39
L(8) ∙c(3,1) ∙ 3/3 = 4∙ ((33−1)/(3−1))∙1 = 52
...
L(13)∙c(3,1) ∙ 1/3 = 3∙ ((33−1)/(3−1))/3 = 13
g│ │ L(g) │k/q│ ∑ ui(j)
──┼──────┼───────┼───┼──────
0│ 000 │ 0 │ 3 │ 0
1│ 001 │ 1 │ 1 │ 13
2│ 002 │ 2 │ 1 │ 26
4│ 011 │ 2 │ 1 │ 26
5│ 012 │ 3 │ 1 │ 39
7│ 021 │ 3 │ 1 │ 39
8│ 022 │ 4 │ 1 │ 52
13│ 111 │ 3 │ 3 │ 13
14│ 112 │ 4 │ 1 │ 52
17│ 122 │ 5 │ 1 │ 65
26│ 222 │ 6 │ 3 │ 26
Součtování v G-systémech
Označme se součet všech e-tých mocnin instancí v daném druhu. Zajímá nás kdy r | se pro všechna e=1..k−1. Podíl se/r označíme malým písmenem, tj. se. V případě, že podíl není beze zbytku možný, zapíšeme na příslušné místo hvězdičku.
G(2,2) s1 G(2,3) s1 s2
──────────── ───────────────────────
0 0
1 2 1 1 2 4 1 3
3 3 6 5 2 10
7
G(2,4) s1 s2 s3
─────────────────────────────────
0
1 2 4 8 1 * 39
3 6 12 9 2 18 180
5 10 1 * 75
7 14 13 11 3 * 441
15
G(2,5) s1 s2 s3 s4
───────────────────────────────────────
0
1 2 4 8 16 1 11 151 2255
3 6 12 24 17 2 34 668 14110
5 10 20 9 18 2 30 506 9102
7 14 28 25 19 3 65 1533 37949
11 22 13 26 21 3 61 1323 29965
15 30 29 27 23 4 104 2794 76748
31
Součtování v R-systémech
Zajímá nás, kdy jsou číslem r dělitelné všechny součty s1,s2,...,sk−1. Následující systémy tuto vlastnost mají. Rozdělíme je podle příslušnosti k Mersennovým (M) nebo Fermatovým (F) systémům.
M-systémy: R(2,2,3), R(2,3,7), R(2,5,31), R(2,7,127), R(3,3,13), R(3,5,121), R(4,2,5), R(4,5,341), R(5,3,31), R(5,5,781), R(6,2,7), R(6,3,43), R(7,5,2801), R(8,2,9), R(8,3,73), R(8,5,4681), R(9,3,91), R(10,2,11), R(11,3,133), R(12,2,13), R(12,3,157),
F-Systémy: R(2,2,3),R(2,4,17)
Všechny uvedené systémy mají buď prvočíselný řád k nebo modul r.
Nejde jen o systémy s prvočíselným modulem r, viz např. M-systém R(9,3,91), kde r = 91 = 7∙13:
R(9,3,91) s1 s2
────────────────────────────────────
0
1 9 81 1 73
2 18 71 1 59
3 27 61 1 49
4 36 51 1 43
5 45 41 1 41
6 54 31 1 43
7 63 21 1 49
8 72 11 1 59
10 90 82 2 164
Součty v R-systémech řádu 3
Zajímá nás, pro které systémy řádu 3 existují mocniné součty 1.a 2. stupně (jako např. v G(2,3)=R(2,3,7), M(3,3)=R(3,3,13),...). Pro druh g dostáváme:
Stupeň Součet
───────────────────────────────────────────────────────
1. g + gn + gn2 = g(1+n+n²) = g (n³−1)/(n−1)
2. (g)² +(gn)²+(gn²)² = g²(1+n²+n4) = g(n6−1)/(n²−1)
Součty 1.stupně jsou dělitelné r:
- V G-systémech G(n,3)=R(n,3,r), r=n³−1, když n = 2 (tj.n−1=1).
- Ve všech M-systémech M(n,3)=R(n,3,r), r=(n³−1)/(n−1).
- V G-systémech G(n,3)=R(n,3,r), r=n³−1, když (n6−1)/(n²−1)/(n³−1) ε N, tj. když (n−1) | (n²−n+1), což je možné jen v případě n=2.
- Ve všech M-systémech M(n,3)=R(n,3,r), r=(n³−1)/(n−1), protože ((n6−1)/(n²−1))/((n³−1)/(n−1))= (n³+1)/(n+1)=(n²−n+1) ε N.