Schematická algebra - Vnořování
Vnořování G-systémů
Vlastní a vnořené druhy
Pro každé d|k existuje systém G(n,d) vnořený do G(n,k). Vnořený druh g' v G(n,k) je podobný svému výchozímu druhu g z G(n,d). (Podobnost zde znamená stejný počet transpozic a obdobnou vnitřní strukturu instancí). Skutečně původní druhy nazýváme vlastní druhy. Systém G(n,p), p je prvočíslo, má právě jeden vnořený systém G(n,1). Pro g z G(n,d), g' z G(n,k), d|k platí: g' = c . g kde c ke koeficient vnoření definovaný následovně:
c(k,d) = (nk−1) / (nd−1)
Do systému G(2,4) se vnořují systémy G(2,1) a G(2,2).
Např. druh g(2) = 1 v G(2,2) vstupuje do G(2,4) jako g(4) = 5 s koeficientem vnoření c(2,4) = 5:
G(2,1):
g(1)=u(0,1)= 0
g(2)=u(0,2)= 1
G(2,2):
g(1)=u(0,1)= 0
g(2)=u(0,2)= 1 u(1,2)= 2
g(3)=u(0,3)= 3
|
G(2,4):
g(1)=u(0,1)= 0
g(2)=u(0,2)= 1 u(1,2)= 2 u(2,2)= 4 u(3,2)= 8
g(3)=u(0,3)= 3 u(1,3)= 6 u(2,3)=12 u(3,3)= 9
g(4)=u(0,4)= 5 u(1,4)=10
g(5)=u(0,5)= 7 u(1,5)=14 u(2,5)=13 u(3,5)=11
g(6)=u(0,6)=15
|
Koeficienty vnoření:
G(2,1) − G(2,2): c(1,2) = (2² −1) / (21 −1) = 3
G(2,2) − G(2,4): c(2,4) = (24 −1) / (2² −1) = 5
 Malá Fermatova věta
Malá Fermatova věta
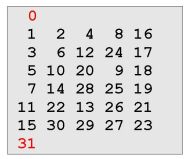
Systém G(n,k) má nk instancí. Všechny druhy g nesoudělné s r=nk−1 (tj. (g,r)=1) jsou druhy vlastní. Do systému G(n,p), p ε P, se vnořuje n instancí (z G(n,1)). Všechny ostatní instance jsou vlastní a mají k transposic. Proto platí tzv.Malá Fermatova věta, p\(np−n) tj.:
np − n ≡ 0 (mod p)
Malou Fermatovu větu dokázal jako první Euler (r.1736). Na obrázku je G(2,5), kde 5 \ (25−2) tj. 5 \ 30.
Z Malé Fermatovy věty pro přirozená čísla plyne také obdobná věta pro cyklická čísla:
(2³−2)+(5³−5)α³ ≡ 0 (mod 3) => (2+5α)³ −(2+5α³) ≡ 0 (mod 3)
Enumerace druhů
Problémem enumerace druhů se zabýval K.F.Gauss v algebraické teorii tříd rovnic [Gauss,II]. Pólya ukázal kombinatorické řešení - odvodil enumerační větu pro počítání tříd s ohledem na libovolné operace symetrie [Preparata,1974]. G-systémy jsou založeny jen na jedné operaci symetrie - rotaci, což umožňuje použít průhlednějších algebraických vztahů.
Nechť v(n,k), w(n,k) a m(n,k) jsou počty vlastních, vnořených a všech druhů v G(n,k).
Platí rekurentní vztahy:
M(n,k) = v(n,k) + w(n,k)
kdev(n,k) = (nk−∑ d∙v(n,d))/k (suma pro d\k)
aw(n,k) = ∑ v(n,d) (suma pro d\k)
Speciálně pro prvočíselný řád p:
M(n,p) = (np + (p−1)∙n)/p
v(n,p) = (np − n)/p
w(n,p) = n
Systém G(2,6)Do systému G(2,6) se vnořují systémy G(2,1), G(2,2) a G(2,3);
G(2,1) je také vnořený do G(2,2) a G(2,3).
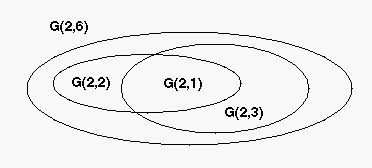 Z celkem 14-ti druhů je 9 druhů vlastních a 5 vnořených.
Z celkem 14-ti druhů je 9 druhů vlastních a 5 vnořených.
Vlastní druhy Vnořené druhy
─────────────────────────────────────────────────────────────────────────────────
v(2,1)=2/1=2 w(2,1)= 0
v(2,2)=(2²−v(2,1))/2=1 w(2,2)= v(2,1) = 2
v(2,3)=(2³−v(2,1))/3=2 w(2,3)= v(2,1) = 2
v(2,6)=(26−v(2,1)−2∙v(2,2)−3∙v(2,3))/6=9 w(2,6)=v(2,1)+v(2,2)+v(2,3)= 5
Proto m(2,6)= v(6) +w(6) = 9 +5 = 14 druhů.
Počet vlastních druhů
Počty vlastní druhů v(n,k) zapsané jako funkce proměnné n:
k v(n,k)
─────────────────────────────────────
1 1/1(n) = n
2 1/2(n²−n)
3 1/3(n³−n)
4 1/4(n4−(n²−n)−n)=¼(n4−n²)
5 1/5(n5−n)
6 1/6(n6−(n³−n)−(n²−n)−n)=1/6(n6−n³−n²+n)
7 1/7(n7−n)
8 1/8(n8−(n4−n²)−(n²−n)−n)=1/8(n8−n4)
9 1/9(n9−n³)
10 1/10(n10−n5−n²+n)
11 1/11(n11−n)
12 1/12(n12−n6−n4+n²)
13 1/13(n13−n)
|
1 2 3 4 5 6 7 8
──────────────────────────────────────────
1 2 3 4 5 6 7 8
0 1 3 6 10 15 21 28
0 2 8 20 40 70 112 168
0 3 18 60 150 315 588 1008
0 6 48 204 624 1554 3360 6552
0 9 116 670 2580 7735 19544 43596
0 18 312 2340 11160 39990 117648 299592
0 30 810 8160 48750 209790 720300 2096640
0 56 ...
0 99 ...
0 186 ...
0 335 ...
0 ...
|
Pro prvočíselná p je:
v(p,p) = pp−1−1
tj. v(p,p)≡−1 mod p. Podíl v(n,p)/n (pεP) odpovídá Fermatovým koeficientům.
Počty vnořených druhů w(n,k) zapsané jako funkce proměnné n:
k w(n,k) ───────────────────────────────────── 1 0 2 n 3 n 4 1/2(n²−n)+1/1(n)= 1/2(n²+ n) 5 n 6 1/3(n³−n)+1/2(n²−n)+1/1(n)=1/6(2n³+3n²+n) 7 n 8 1/4(n4−n²)+1/2(n²−n)+n = 1/4(n4+n²+2n) |
1 2 3 4 5 6 7 8 ───────────────────────────────────── 0 0 0 0 5 6 7 8 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 1 3 6 10 15 21 28 36 1 2 3 4 5 6 7 8 1 5 14 30 55 91 140 204 1 2 3 4 5 6 7 8 1 6 24 70 165 336 616 1044 |
Rozepišme uvedené rekurentní vztahy pro počet všech druhů. Počty všech druhů m(n,k) zapsané jako funkce proměnné n:
k m(n,k) ───────────────────────────────────────── 1 1/1(n) + 0 = n 2 1/2(n²− n)+ n = 1/2 (n²+n) 3 1/3(n³−n)+ n = 1/3 (n³+ 2n) 4 1/4(n4−n2)+ 1/2 (n²+n)=1/4 (n4+ n²+2n) 5 1/5(n5−n) + n = 1/5 (n5+ 4n) 6 1/6(n6−n³−n²+n+2n³+3n²+n)=1/6(n6+n³+2n²+2n) 7 1/7(n7−n) + n = 1/7 (n7+ 6n) 8 1/8(n8−n4)+1/4(n4+n²+2n)=1/8(n8+n4+2n²+4n) |
1 2 3 4 5 6 7 8 ───────────────────────────────────────── 1 2 3 4 5 6 7 8 1 3 6 10 15 21 28 36 1 4 11 24 45 76 119 176 1 6 24 70 165 336 616 1044 1 8 51 208 629 1560 3367 6560 1 14 130 700 2635 7826 19684 43800 1 20 315 2344 11165 39996 117655 299600 1 36 834 8230 48915 210126 720916 209768 |
Výrazy v závorkách vpravo (n, n²+n, n³+ 2n, n5+ 4n,..) nemají nikdy absolutní člen, tedy platí:
k∙m(n,k) ≡ 0 (mod n)
Pro prvočíselná p je:
m(p,p) = pp−1+p−1
tj. m(p,p)≡−1 mod p.
Rozdílové posloupnosti v G-systémech
Posloupnosti v(n,k) i m(n,k) (n=1,2,3..) tvoří pro každé k
aritmetické posloupnosti řádu k.
Konstanta poslední rozdílové posloupnosti má hodnotu:
První rozdílová posloupnost m(n,k) je podobná posloupnosti nk−1.
m(n,3) n² ──────────────────── ────────────────── 1,4,11,24,45,76,... ....... 3,7,13,21,31,... 1,4,9,16,25,36,... 4,6, 8,10,... 3,5,7,9,11,.. 2,2,2,,.... 2,2,2,2,...
Řády k i konstanty d(k) těchto posloupností jsou stejné.
Pro počet vlastních druhů v G-systému G(p) platí:
v(p,i+p) + (−1)p ∙ v(p,i) ≡ −1 (mod p)
Např. pro p = 5, a(i)=v(5,i): a(0) = 0; a(1) = 6; a(2) = 48; a(3) =
204; a(4) = 624; a(5) = 1554;
tj. a(5)−a(0)= 1554 ≡ (−1) mod 5 (viz periodické
posloupnosti).
| Messiaen Olivier [], 1908-1992, francouzský skladatel mystické hudby s výraznou melodikou. Pracoval s modalitami, které mají omezený počet transpozic. |
Do systému G(2,12) je vnořeno celkem 17 druhů, představujících celkem 2∙1+1∙2+2∙3+3∙4+9∙6 = 76 instancí.
Systém Distanční schéma Příklad Pojmenování
────────────────────────────────────────────────────────────────────────
G(2,1):
0 0(0) Ticho
4095 11111…1(1) c,c#,d,d#,e,…,a#,h Dvanáctizvuk
G(2,2):
1365 22222(2) c,d,e,f#,g#,a# Celotónová stupnice
G(2,3):
585 333(3) c,d#,f#,a Zmenšený septakord
1755 1212121(2) c,c#,d#,e,f#,g,a,a# Inverze zm.septakordu
G(2,4):
273 44(4) c,e,g# Zvětšený kvintakord
819 13131(3) c,c#,e,f,g#,a
1911 11211211(2) c,c#,d,e,f,f#,g#,a,a# Inv.zv.kvintakordu
G(2,6):
65 6(6) c,f# Triton
195 151(5) c,c#,f#,g .
325 242(4) c,d,f#,g# ..
455 11411(4) c,c#,d,f#,g,g# Messiaenovy mody
715 12312(3) c,c#,d#,f#,g,a omezených transpozic
845 21321(3) c,d,d#,f#,g#,a ...
975 1113111(3) c,c#,d,d#,f#,g,g#,a ..
1495 1122112(2) c,c#,d,e,f#,g,g#,a# .
2015 111121111(2) c,c#,d,d#,e,f#,g,g#,a,a# Inverze tritonu
| Janeček Karel , 1903-1974, český hudební teoretik a skladatel (tvůrce klavírní, komorní, vokální i orchestrální hudby). Jeden z největších českých hudebních teoretiků, systematik. Zabýval se teorií skladby a harmonií hudby, klasickou i moderní. Systematicky vypsal všechny možné souzvuky 12-ti tónové soustavy a ohodnotil je několika charakteristikami. Věnoval se hudební tektonice, hudebním formám, nauce o melodii, analýze hudebních skladeb a také otázkám kompoziční představivosti, talentu,... Myšlenky svých předchůdců zobecnil a přesněji formuloval, principy dokládal úkázkami z hudebních děl. |
Počet druhů souzvuků
Dříve odvozené vztahy dávají v případě n=2 tyto hodnoty:k v(2,k) w(2,k) m(2,k) ────────────────────────── 1 2 0 2 2 1 2 3 3 2 2 4 4 3 3 6 5 6 2 8 6 9 5 14 7 18 2 20 8 30 6 36 9 56 4 60 10 99 9 108 11 186 2 188 12 335 17 352
Celkem je v hudební 12-ti tónové soustavě 4096−76=4020 vlastních instancí, tj. uskupení se všemi 12-ti transpozicemi. Tato uskupení tvoří 4020/12 = 335 druhů. Dohromady je proto v hudební soustavě 335+17 = 352 druhů.
Počet druhů ve velkých systémech
V menších systémech G(2,k) odpovídá počet druhů přibližně počtu možností jak rozdělit číslo k v součet přirozených čísel p(k) (viz Rozdělení čísla na sčítance):
m(2,k) ~ p(k)
Např. systém G(2,4) (viz Binární G-systémy/ Distanční schemata) je
tvořen druhy odpovídajícími součtům: 4,3+1,2+2,2+1+1,1+1+1+1 a nulovým
druhem.
Pro vyšší hodnoty k roste m(2,k) rychleji než p(k)
Např. v G(2,6) se součet 2+2+1+1 rozpadá na dva druhy: 1,2,1,2 a 1,1,2,2.
Proto bude
m(2,k) > p(k).
K odhadu počtu druhů ve velkých G-systémech se pokusíme využít věty o rozložení prvočísel (viz Prvočíselná věta).
Pro velká r platí přibližně: π(r) = r/ln(r), π(r)∙ln(r) = r, eln(r)∙π(r) = er (eln(r))π(r) = er, rπ(r) = er
tj.:
r ~ ln(rπ(r))
Uvažujme nyní případ r=nk. Po dosazení, úpravě a k-tém odmocnění: rπ(r) = er, (nk)π(nk) = e(nk), n(k∙π(nk)) = e(nk), nπ(nk) = e(nk/k)
Pro velká r dává výraz nk/k přibližně počet druhů m systému G(n,k).
Přibližně proto platí: nπ(r) = em, ln(nπ(r)) = m
m ~ π(r)∙ ln(n)
kde n je základ, r modul a m počet druhů systému G(n,k).
Např. pro n=10, k=3, tj. r=1000 a π(r)=168. Hrubý odhad pro počet druhů v G(10,3) je m=π(r)∙ ln(n)=168 ∙ ln(10) = 387.
Pólyova enumerace
Pólzova enumerace se zabývá určováním počtu možných rozdělení množiny do ekvivalentních tříd. Byla s úspěchem aplikována na popis stávajících i předpověď nových chemických struktur... Umožňuje vyčíslit počet tříd ekvivalence libovolně-rozměrného útvaru jen na základě operací symetrie, které jsou pro daný útvar povoleny.
Postup výpočtu
Postup výpočtu celkového počtu druhů podle Pólyovy teorie:
Určit povolené operace symetrie (rotace, překlopení, osová symetrie,...) Ke každé operaci najít počet fixovaných instancí, tj. instancí které se po provedení operace nezmění (zůstanou fixovány) Podle stanovených pravidel sestavit tzv. cyklový index (polynom cyklů), Do polynomu dosadit, výsledek dává celkový počet druhůV případě rotačních operací dává Pólyova teorie [Beckenbach] výsledek:
m(n,k)=1/k ∑φ(d)∙ nk/d for d|k, d≤k
kde φ je Eulerova funkce.
Pólya, Győrgy| Pólya, Győrgy [poja], 1887-1985, maďarský matematik humanitního vzdělání a osobitého stylu výkladu. Jeho matematické dílo je rozsáhlé a dotýká se celé řady oborů. Známá je jeho enumerační věta z r.1937. Zabýval se také metodami výuky matematiky. |
Základem vztahu je následující schéma fixovaných instancí:
G(2,4) 0 * * * 1 2 4 8 3 6 12 9 5 10 * * 7 14 13 11 15 * * *
K existujícím instancím se (součtem na pravé straně) připojí další (označené hvězdičkami).
Všechny instance (o počtu S) vytvoří obdélník šířky k a výšky m, proto m = S/k.
Hodnota m(n,k) (tj. celkový počet druhů) bývá také nazývána počet cyklických permutací k-té třídy z n prvků s opakováním.
Charakteristiky permutací
Indikátorem cyklů permutace nazýváme polynom sestavený z cyklového typu tak, že délka d každého cyklu je indexem a počet cyklů p dané délky exponentem výrazu (xdp). Indikátor cyklů grupy I(x) je součtem indikátorů jednotlivých permutací.
Např. prvky grupy permutací 3 třídy mají následující charakteristiky:
Permutace Cykly a řád Délky Parita Typ a indikátor
──────────────────────────────────────────────────────────────
p0 123 (1)(2)(3) 1 1 1 even (+) (3,0,0)
123 1 x1³
──────────────────────────────────────────────────────────────
p1 123 (1) (2,3) 1 2 odd (−) (1,1,0)
132 2 x11+x21
──────────────────────────────────────────────────────────────
p2 123 (1,2,3) 3 even (+) (0,0,1)
231 3 x31
───────────────────────────────────────────────────────────────
p3 123 (2) (1,3) 1 2 odd (−) (1,1,0)
321 2 x11+x21
───────────────────────────────────────────────────────────────
p4 123 (1,3,2) 3 even (+) (0,0,1)
312 3 x31
──────────────────────────────────────────────────────────────
p5 123 (3) (1,2) 1 2 odd (−) (1,1,0)
213 2 x11+x21
Indikátor cyklů
V případě permutační grupy označíme indikátor cyklů T(x).
Pro P(3) je:
T3(x)= (x1³)+ (x11
+x21)+ (x31)+
(x11 +x21)+
(x31) + (x11
+x21)
tj.T3(x) = x1³ +
3x1x2 + 2x3
Obecně pro P(k) dostaneme následující vztahy: T1(x) = x1 T2(x) = x1² + x2 T3(x) = x1³ + 3x1∙x2 + 2x3 T4(x) = x14 + 6x1²∙x2 + 3x2² + 8x1∙x3 + 6x4 T5(x) = x15 + 10x1³∙x2 +15x1∙x2² +20x1²∙x3 + 20x2∙x3 + 30x1∙x4 + 24x5
Koeficienty těchto polynomů se získávají pomocí tzv.Cauchyho formule (viz dále).
Derivace indikátoru cyklů
Pro parciální derivace uvedených polynomů podle
x1,x2,.. platí některé vztahy.
Vyčísleme parciální derivace indikátoru cyklů v P(3):
d(x1³ + 3x1∙x2 +
2x3)/ dx3 = 2
[=(3−1)!]
d(x1³ + 3x1∙x2 +
2x3)/ dx2 = 3x1
[=3∙(3−2)!x1]
d(x1³ + 3x1∙x2 +
2x3)/ dx1 = 3x1²+
3x2 [...]
Obecně platí například [Riordan]: dT(x)/dxn = (n−1)! dT(x)/dxn−1 = n∙(n−2)!x1
Cyklový index
Součtem indikátorů jednotlivých permutací je P(x) = x1³ + 2∙x31. Uvedené permutace zachovávají posloupnost prvků 1−2−3−1−2−3... a odpovídají proto rotacím. A právě na rotacích jsou založené G-systémy.
Podle Polyovy enumerace je počet druhů určen tzv.cyklovým indexem. Cyklový index grupy M(x) je definován jako podíl indikátoru cyklů grupy a řádu grupy, tj.
M(x) = P(x)/k
kde k je počet operací symetrie. V našem případě se jedná o tři rotace (k=3). Za x budeme dosazovat počet prvků (n).V G(n,3) tak dostaneme: m(n,3) = (n³ + 2∙n)/3.
Pro n=2 resp.3 je tedy: m(2,3) = (8+4)/3 = 4, resp. m(3,3) = (27+6)/3 = 11.
Čtenář se může přesvědčit, že výsledky odpovídají hodnotám získaným rekurentním výpočtem (v odstavci Enumerace druhů/Počet všech druhů).
Podstata enumerace
Rozložení prvků v k-vrcholech je považováno za fixované vzhledem k určité operaci, když po provedení této operace zůstane v každém vrcholu týž prvek jako před provedením operace. V uvedeném vztahu m(n,3) = (n³ + 2∙n)/3 doplňuje činitel 2∙n fixované instance.
K systému G(2,3) přísluší 4 fixované instance (označené hvězdičkami):
G(2,3) 0 * * 1 2 4 3 6 5 7 * *
Složení R-systémů
R-systémy s daným modulem
Pro prvočíselný modul existují vždy dva triviální systémy a několik dvojic duálních systémů. Např. pro r=13 jde o triviální systémy R(1,1,13), R(12,2,13) a níže vypsané (v řazení podle řádu k) duální systémy se stupni nε{1..r−1}:
k=3
R(3,3,13) R(9,3,13)
0 0
1 3 9 1 9 3
2 6 5 2 5 6 φ(3)=2
4 12 10 4 10 12
7 8 11 7 11 8
13 13
R(5,4,13) R(8,4,13)
0 0
1 5 12 8 1 8 12 5
2 10 11 3 2 3 11 10 φ(4)=2
4 7 9 6 4 6 9 7
13 13
R(4,6,13) R(10,6,13)
0 0
1 4 3 12 9 10 1 10 9 12 3 4
2 8 6 11 5 7 2 7 5 11 6 8 φ(6)=2
13 13
R(2,12,13)
0
1 2 4 8 3 6 12 11 9 5 10 7
13
R(6,12,13)
0
1 6 10 8 9 2 12 7 3 5 4 11
13 φ(12)=4
R(7,12,13)
0
1 7 10 5 9 11 12 6 3 8 4 2
13
R(11,12,13)
0
1 11 4 5 3 7 12 2 9 8 10 6
13
Nejvyšším řádem pro prvočíselné rεP je k= r−1.
Řády jednotlivých systémů jsou čísla k, která dělí číslo r−1: k|(r−1). V našem případě dělitelé čísla 12, tj. 1,2,3,4,6 a 12. Systémů s daným řádem k je φ(k): k 1 2 3 4 6 12 φ(k) 1 1 2 2 2 4
Permutace R-systémů
Všechny systémy téhož řádu jsou si podobné. Čísla v řádcích zůstávají stejná, jen se různě přeskupují. Např. systémy R(3,3,13) a R(9,3,13), se liší jen pořadím druhého a třetího sloupce. R(3,3,13): R(9,3,13): 0 0 1 3 9 1 9 3 ... ...
Přeskupení čísel {1,3,9} a {1,9,3} sestává ze dvou cyklů: jednoho
elementárního (délky 1) a jednoho délky 2. Permutaci zapíšeme symbolicky
[1][3,9].
Obdobně postupujeme i pro další řády k:
R(3,3,13): 1 3 9 k = 3
R(9,3,13): 1 9 3
cykly: [1][3,9]
───────────────────────────────────
R(5,4,13): 1 5 12 8 k = 4
R(8,4,13): 1 8 12 5
cykly: [1][12][5,8]
───────────────────────────────────
R( 4,6,13): 1 4 3 12 9 10 k = 6
R(10,6,13): 1 10 9 12 3 4
cykly: [1][12][3,9][4,10]
───────────────────────────────────────────────────────────
R( 2,12,13): 1 2 4 8 3 6 12 11 9 5 10 7
R( 6,12,13): 1 6 10 8 9 2 12 7 3 5 4 11 k = 12
R( 7,12,13): 1 7 10 5 9 11 12 6 3 8 4 2
R(11,12,13): 1 11 4 5 3 7 12 2 9 8 10 6
cykly: [1][12][3,9][5,8][4,10][2,6,11,7]
Věta o složení R-systémů
Nechť d je dělitel řádu k, d|k. Cykly systému R(n,d,r) jsou
podmožinou cyklů R(n,k,r).
Např. [1][3,9] (d=3) je podmnožinou [1][12][3,9][4,10] (k=6) protože
d|k.
Čísla uvnitř závorek udávají jaké základy mají systémy, jejichž
čísla permutujeme. Zahrnují jak základy vnořených systémů, tak i vlastní
permutaci základů daného řádu.
Pro k=12 existují vnořené permutace [1][12][3,9][5,8][4,10] a vlastní
permutace [2,6,11,7].
| Euler, Leonard [ojler], 1707-1783, švýcarský matematik a fyzik, jeden z největších matematiků všech dob. Zabýval se teoretickou matematikou i jejími aplikacemi (mechanikou, astronomií, optikou, kartografií, hudební teorií,...) Věnoval se teorii čísel, diferenciálnímu, integrálnímu i variačnímu počtu. Objevil metodu řešení bikvadratické rovnice. Zasáhl snad do všech oblastí matematiky, mnohdy zcela originálním způsobem. Mnohé jím zavedené symboly se používají dodnes (i=√−1, ∑f(x),...). Po oslepnutí r.1766 své práce diktoval. |
Protože vlastní permutace je vždy jen jedna, je jednotlivých cyklů
právě σ(k), kde sigma;(k) je počet dělitelů čísla k.
Pro k=12 je σ(12) = 6 a jednotlivým dělitelům odpovídají permutace:
d= 1: [1] φ( 1) = 1
d= 2: [12] φ( 2) = 1
d= 3: [3,9] φ( 3) = 2
d= 4: [5,8] φ( 4) = 2
d= 6: [4,10] φ( 6) = 2
d=12: [2,6,11,7] φ(12) = 4
Každá vlastní permutace řádu k má právě φ(k) prvků. Každý prvek je
základem jednoho systému.
R( 2,12,13): 2 6 11 7
R( 6,12,13): 6 2 7 11
R( 7,12,13): 7 11 6 2
R(11,12,13): 11 7 2 6
Hodnoty φ(d) jednotlivých dělitelů d|k postupně utvářejí řád k.
Pro k=12 je: φ(1)+φ(2)+φ(3)+φ(4)+φ(6)+φ(12) = 1+1+2+2+2+4 = r−1 =12.
Obecně platí (Eulerova-Gaussova) věta, kterou budeme nazývat věta o složení R-systémů:
∑(φ(d)) = a; for d|a (d>0)
tj. každé číslo a je součtem φ(d) všech svých dělitelů.
Vnořování R-systémů
Porovnání s G-systémy
Stejně jako u G-systémů i v R-systémech člení kongruence (G-relace) množinu všech instancí {0..r} na druhy. Ukazují se vlastní a vnořené druhy a podobné zákonitosti výstavby.
Začneme případem, kdy nεP a čísla r nejsou násobky n (tj. není n|r) [Gauss II].
Mějme např. r=63 a porovnejme systém R(13,6,63) s G-systémem G(2,6)= R(2,6,63):
G(2,6)=R(2,6,63) R(13,6,63):
0 0
1 2 4 8 16 32 1 13 43 55 22 34
3 6 12 24 48 33 2 26 23 47 44 5
5 10 20 40 17 34 3 39
7 14 28 56 49 35 4 52 46 31 25 10
9 18 36 6 15
11 22 44 25 50 37 7 28 49
13 26 52 41 19 38 8 41 29 62 50 20
15 30 60 57 51 39 9 54
21 42 11 17 32 38 53 59
23 46 29 58 53 43 12 30
27 54 45 14 56 35
31 62 61 59 55 47 16 19 58 61 37 40
63 18 45
21
24 60
27 36
33 51
42
48 57
63
Modul obou systémů (r=63) je tentýž. Proč je každý z těchto systémů jiný, v čem se liší? Jaké druhy se vnořují do R(13,6,63)?
Princip vnořování
Vnořování G-systémů je určeno koeficientem vnoření c(k,d)=(nk−1)/(nd−1) = r/(nd−1) (viz..) Pro G(2,6) je c(d,6)= r/(2d−1), kde d=1,2 nebo 3. Pro R(13,6,63) ale hodnoty (13d−1) číslo r=63 nedělí...
 Číslo r=63 se dělí
hodnotami(13d−1) jen do té míry, pokud je to možné. O dělení
rozhoduje vždy největší společný dělitel (r,13d−1):
(131−1,r)= (13−1,63) = (12,63) = 3
(13²−1,r)= (169−1,63) = (168,63) = 21
(13³−1,r)= (2197−1,63)= (2196,63)= 9
Číslo r=63 se dělí
hodnotami(13d−1) jen do té míry, pokud je to možné. O dělení
rozhoduje vždy největší společný dělitel (r,13d−1):
(131−1,r)= (13−1,63) = (12,63) = 3
(13²−1,r)= (169−1,63) = (168,63) = 21
(13³−1,r)= (2197−1,63)= (2196,63)= 9
Do systému R(13,6,63) se vnořují následující 3 systémy:
r=3: (q=21) r=21: (q=3)
0 0
1 1 13
2 2 5
3 3 18
4 10
r=9: (q=7) 6 15
0 7
1 4 7 8 20
2 8 5 9 12
3 11 17
6 14
9 16 19
21
Koeficient vnoření
Koeficient vnoření c(k,d) pro vnořování systémů s řádem d | k do R-systému R(n,k,r) definujeme:
c(k,d) = r / (nd−1,r)
V našem příkladě R(13,6,63) je: c(6,1) = 63 / (131−1,r) = 63/3 = 21 c(6,2) = 63 / (13²−1,r) = 63/21 = 3 c(6,3) = 63 / (13³−1,r) = 63/9 = 7
Vnořené instance
Započítáme-li do vnořovaných systémů G(2,6) všechny instance, tj. i instance vnořené z nižších systémů dostaneme: při d=1: 21=2 instance: 0,63 při d=2: 2²=4 instance: 0,21,42,63 při d=3: 2³=8 instancí: 0,9,18,27,36,45,54,63
|
Když ν=63 a p=13, pak m=6. Proto x63−1 bude mít podle modulu 13 prosté součinitele šestého, třetího, druhého a prvního stupně. Ale součin činitelů prvního stupně je společným dělitelem (vyššího stupně) funkcí x63−1 a x12−1, tj.x³−1. Proto existují 3 součinitelé prvního stupně. Součin všech prvočinitelů druhého a prvního stupně bude společným dělitelem funkcí x63−1 a x168−1, tj. bude roven x21−1; proto existuje (21−3)/2=9 součinitelů druhého stupně. Součin prvočinitelů třetího a prvního stupně bude společným dělitelem funkcí x63−1 a x2196−1, tj. roven x9−1; proto existují (9−3)/3=2 dělitelé třetího stupně. Nakonec ostatní jsou šestého stupně a jejich počet je podle toho roven (63−6−18−3)/6, tj. 6. |
V R(13,6,63) obdobně najdeme: při d=1: 4 instance: 0,21,42,63 při d=2: 22 instancí: 0,3,6,9,12,...54,57,60,63 při d=3: 10 instancí: 0,7,14,21,28,35,42,49,56,63
Pro d=1,2 resp. 3 jde o násobky 21,3 resp. 7.
Enumerace počtu druhů
Z předchozího odstavce plyne přímo i postup jak spočítat druhy v systémech R(n,k,r) [GaussII]:
K.F.Gauss (na rozdíl od naší konvence) nezapočítává do počtu druhů číslo 0.
Vnořování M-systémů
Případ k=1M(4,3) 0 1 4 16 2 8 11 3 12 6 5 20 17 7 9 15 18 10 19 13 14 21
Při k=1 je vždy r=(n1−1)/(n−1)=1 a všechny systémy M(n,1) jsou stejné, mají 2 instance {0,1}. Ale jejich vnořování neprobíhá tak jako u G-systémů. Systém M(4,3), tj.k=3 vnořuje ze systému M(4,1) instance čtyři {0,7,14,21}:
Obecně se do M(n,k) vždy vnořuje w1 druhů z M(n,1), kde:
w1 = (n−1,k)+1
V případě n=2 (G-systémy) je w1 =(1,k)+1 = 1+1 = 2 (= n).
Vnořování M-systémů M(n,d) s řádem d|k do systému M(n,k) probíhá
analogicky jako u G-systémů jedině v případě (n−1,k)=1. Za této podmínky
vnořují M-systémy s vyšším řádem k do sebe M-systémy s nižším řádem
d:
M(4,1) → M(4,2) → M(4,4) → M(4,8)
M(3,1) → M(3,3) → M(3,9) ...
V případě, že k je prvočíslo, má M-systém všechny druhy vlastní, až
na 2 druhy vnořené ze systému 1.
Např. M(3,3)
0
1 3 9
2 6 5
4 12 10
7 8 11
13
Má tedy celkem (nk−1)/(n−1)+1−2 =(nk−1)/(n−1) −1 = (nk−n)/(n−1) vlastních instancí a (nk−n)/(n−1)/k vlastních druhů.
0
13 65
26 130
39
52 104
78
91 143
117
156
Není-li podmínka (n−1,k)=1 splněna, vnořuje se do M-systému obecně jiný počet druhů než má příslušný M-systém. V některých triviálních případech se místo M-systému M(n,d) vnořuje G-systém G(n,d) Např. M(3,2) + G(3,3) M(3,6), G(4,2) + M(4,3) => M(4,6).
Obecně ale vnořená struktura nemusí mít ani tvar M-systému ani G-systému. Např. M(5,4) má 13 vnořených druhů, které netvoří ani M systém M(5,2), s (5²−1)/(5−1)+1 = 24/4+1 = 7 instancemi ani G(5,2) s 5² = 25 instancemi.
Koeficient vnoření
V uvedeném příkladu druhů vnořených do systému M(5,4) vidíme, že druhy ze systému řádu k= 1 se vnořují s koeficientem c(4,1)= 39 a druhy ze systému řádu k= 2 s koeficientem c(4,2)= 13.
Odtud odhadujeme vztah:
c(k,d)= (nk−1)/(nd−1)/(n−1,k/d)
V našem příkladě: c(4,1)= (54−1)/(51−1)/(5−1,4/1) = 624/4/(4,4) = 624/16 = 39 c(4,2)= (54−1)/(5²−1)/(5−1,4/2) = 624/24/(4,2) = 624/48 = 13
V kapitole o R-systémech jsme formulovali Gaussův obecný vztah pro koeficient vnoření:
c(k,d) = r / (nd−1,r)
Pro M-systémy je r = (nk−1)/(n−1).
V našem příkladu je r = (54−1)/(5−1) = 624/4 = 156. c(4,1)= r/(51−1,r) = 156/(4,156) = 156/4 = 39 c(4,2)= r/(5²−1,r) = 156/(24,156) = 156/12 = 13
Porovnání
Z předchozího odstavce máme 2 vztahy pro koeficient vnoření. Pokud platí oba zároveň musí být: (nk−1)/(nd−1)/(n−1,k/d) = (nk−1)/(n−1)/(nd−1,(nk−1)/(n−1)) tj. (n−1,k/d) = (nd−1,(nk−1)/(n−1)) / ((nd−1)/(n−1)).
Při označení r(i) = (ni−1)/(i−1) vztah přepíšemena:
(nd−1, r(k)) = r(d)∙(n−1,k/d)
Enumerace druhů
Systém M(3,6) má tyto vnořené druhy ze systémů M(n,d), d|k:
0
14 42 126
28 84 252
56 168 140
70 210 266
91 273
98 294 154
112 336 280
182
196 224 308
238 350 322
364
Ze systému řádu d=1 pochází m1=(n−1,k)+1 = (2,6)+1 = 3 instance,
tj. 3 druhy s jednou transpozicí: 0 182 364
Pro systém řádu d=2 je hodnota t=(n−1)/(n−1,k/d) =2/(2,3) = 2. Vnořené schéma má celkem m2= (nd−1)/t+1 = (3²−1)/2+1 = 5 instancí: 0 91 273 182 364
Protože t=n−1, tvoří vnořené schéma M-systém M(3,2). Tři instance ale patří, jak jsme viděli, systému řádu d=1. Tedy přibíráme jen 5−3=2 nové instance, které tvoří 2/d = 1 druh.
0
14 42 126
28 84 252
56 168 140
70 210 266
98 294 154
112 336 280
182
196 224 308
238 350 322
364
V systému řádu d=3 je parametr t=(n−1)/(n−1,k/d) =2/(2,2) = 1. Vnořené schéma má celkem m3= (nd−1)/t+1 = (3³−1)/1+1 = 27 instancí.
Protože t=1, tvoří vnořené schéma G-systém G(3,3). Tři instance ale opět patří systému řádu d=1. Tedy přibíráme 27−3=24 nové instance, které tvoří 24/d = 8 druhů.
Nyní víme, že do systému M(3,6) vchází 3+1+8 = 12 druhů, které tvoří 3∙1 + 1∙2 + 8∙3 = 3+2+24 = 29 instancí. Zadaný M-systém má celkem m6 = (nk−1)/(n−1)+1 = (36−1)/2+1 = 365 instancí. (Nemuseli jsme počítat parametr t. Víme, že jde o M-systém a v tom případě je vždy t=n−1.)
Po odečtení vnořených instancí dostáváme 365−29 = 336 instancí členěných do 336/k = 56 druhů.
Systém M(3,6) má tedy 56 vlastních a 12 vnořených druhů, tj. celkem 68 druhů.
Počet druhů
v(n):
k\n 1 2 3 4 5 6 7 8
─────────────────────────────────────────────────
1
2 1 1 2 2 3 3 4
3 2 4 6 10 14 18 24
4 3 8 20 36 63 96 144
5 6 24 68 156 310 560 936
6 9 56 222 640 1547 3246 6228
w(n):
k\n 1 2 3 4 5 6 7 8
─────────────────────────────────────────────────
1
2 2 3 2 3 2 3 2
3 2 2 4 2 2 4 2
4 3 6 4 9 5 10 6
5 2 2 2 2 6 2 2
6 5 12 16 25 19 52 30
m(n):
k\n 1 2 3 4 5 6 7 8
─────────────────────────────────────────────────
1
2 3 4 4 5 5 6 6
3 4 6 10 12 16 22 26
4 6 14 24 45 68 106 150
5 8 26 70 158 316 562 938
6 14 68 238 665 1566 3298 6258
Vnořování F-systémů
Vlastní druhy
Vlastní druhy v F-systémech mají 2h transpozic. (Proto jsme zvolili při definici v exponentu písmeno h místo k). Pro řád k F-systému F(n,h)=R(n,k,r) platí:
k=2h
Systém R(n,k,r) nemůže mít více než φ(r) transpozic, tedy 2h ≤ φ(nh+1).
Systémy s exponentem h=2t
V těchto systémech existuje w = 2+(n mod 2) vnořených druhů.
Systémy s prvočíselným exponentem
Do systémů s prvočíselným h se vnořuje druhů.
w = 2+ (n+1) div 2
Počet vlastních druhů:
v = (nh−n)/2h
Např. v F(2,11) je n=2, h=11 a r=211+1 = 2049. Do systému se vnořují w = 2+ (n+1) div 2 = 2 + 1 = 3 druhy.
Vlastních druhů je v = (nh−n)/2h = (2048−2)/22 = 93.
Systémy s prvočíselným modulem
Když r=(nh+1)ε P pak:
w = 2
v = nh/2h
Proto pro (n,h)= 1 nemůže být nikdy rεP.Vnořování multiplikativních tabulek
Multiplikativní tabulky
Tabulky T(k) čísel m*n mod k, např.:
T1 T2 T3 T4 T5
1 1 2 1 2 3 1 2 3 4
2 1 2 0 2 2 4 1 3
3 2 1 3 1 4 2
4 3 2 1
T6 T7 T8
1 2 3 4 5 1 2 3 4 5 6 1 2 3 4 5 6 7
2 4 0 2 4 2 4 6 1 3 5 2 4 6 0 2 4 6
3 0 3 0 3 3 6 2 5 1 4 3 6 1 4 7 2 5
4 2 0 4 2 4 1 5 2 6 3 4 0 4 0 4 0 4
5 4 3 2 1 5 3 1 6 4 2 5 2 7 4 1 6 3
6 5 4 3 2 1 6 4 2 0 6 4 2
7 6 5 4 3 2 1
T9 T10
1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9
2 4 6 8 1 3 5 7 2 4 6 8 0 2 4 6 8
3 6 0 3 6 0 3 6 3 6 9 2 5 8 1 4 7
4 8 3 7 2 6 1 5 4 8 2 6 0 4 8 2 6
5 1 6 2 7 3 8 4 5 0 5 0 5 0 5 0 5
6 3 0 6 3 0 6 3 6 2 8 4 0 6 2 8 4
7 5 3 1 8 6 4 2 7 4 1 8 5 2 9 6 3
8 7 6 5 4 3 2 1 8 6 4 2 0 8 6 4 2
9 8 7 6 5 4 3 2 1
T11 T12
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11
2 4 6 8 10 1 3 5 7 9 2 4 6 8 10 0 2 4 6 8 10
3 6 9 1 4 7 10 2 5 8 3 6 9 0 3 6 9 0 3 6 9
4 8 1 5 9 2 6 10 3 7 4 8 0 4 8 0 4 8 0 4 8
5 10 4 9 3 8 2 7 1 6 5 10 3 8 1 6 11 4 9 2 7
6 1 7 2 8 3 9 4 10 5 6 0 6 0 6 0 6 0 6 0 6
7 3 10 6 2 9 5 1 8 4 7 2 9 4 11 6 1 8 3 10 5
8 5 2 10 7 4 1 9 6 3 8 4 0 8 4 0 8 4 0 8 4
9 7 5 3 1 10 8 6 4 2 9 6 3 0 9 6 3 0 9 6 3
10 9 8 7 6 5 4 3 2 1 10 8 6 4 2 0 10 8 6 4 2
11 10 9 8 7 6 5 4 3 2 1
Vlastní instance
Zde můžeme (podobně jako v G-systemech) najít čísla,
která jsou vlastní, ne vnořená.
(Viz výše - rřádky a sloupce, které neobsahují číslo 0.)
Tabulky vlastních instancí mají φ(k) řádek a sloupců, φ je Eulerova funkce.
T1 T2 x 1 T3 T4 T6 1 2 1 3 1 5 2 1 3 1 5 1
T5 T8 T10 T12
1 2 3 4 1 3 5 7 1 3 7 9 1 5 7 11
2 4 1 3 3 1 7 5 3 9 1 7 5 1 11 7
3 1 4 2 5 7 1 3 7 1 9 3 7 11 1 5
4 3 2 1 7 5 3 1 9 7 3 1 11 7 5 1
T7 T9 1 2 3 4 5 6 1 2 4 5 7 8 2 4 6 1 3 5 2 4 8 1 5 7 3 6 2 5 1 4 4 8 7 2 1 5 4 1 5 2 6 3 5 1 2 7 8 4 5 3 1 6 4 2 7 5 1 8 4 2 6 5 4 3 2 1 8 7 5 4 2 1
T11 1 2 3 4 5 6 7 8 9 10 2 4 6 8 10 1 3 5 7 9 3 6 9 1 4 7 10 2 5 8 4 8 1 5 9 2 6 10 3 7 5 10 4 9 3 8 2 7 1 6 6 1 7 2 8 3 9 4 10 5 7 3 10 6 2 9 5 1 8 4 8 5 2 10 7 4 1 9 6 3 9 7 5 3 1 10 8 6 4 2 10 9 8 7 6 5 4 3 2 1