Konfigurace planet
Pýthagorás ze Samu| Pýthagorás ze Samu , cca 575-509 před.n.l., antický řecký matematik, zakladatel filozofické školy. Podle jeho učení vládne harmonie hudbě, pohybům nebeských těles, mikrosvětu i lidské duši samé. |
Harmonie sfér
Svůj objev – že zvuky, jejichž frekvence jsou v poměru malých celých čísel vytváří konsonantní (libozvučná) souznění – považoval Pýthagorás za tak zásadní, že si troufl jej zobecnit na pohyby v celém kosmu .
Podle Pýthagora vytváří pohyb planet souznění – “harmonii sfér”, zvuk této kosmické harmonie ale neslyšíme, protože jsme mu již od narození přivykli…
První, komu se podařilo posunout Pýthagorovu představu o kousek dál byl Johannes Kepler. J.Kepler zkoumal poměry vzdáleností planet od Slunce (sférám oběhu planet se pokusil vepsat a opsat některá pravidelná tělesa) a poměry rychlostí planet. Věřil, že každé planetární sféře přísluší jeden tón stupnice.
J.Kepler nakonec našel určité poměry blízké celočíselným v poměrech rychlostí planet v přísluní a odsluní. Rychlosti planet v přísluní a odsluní však závisí na excetricitě (výstřednosti) eliptické dráhy planety a ta se v čase mění. Např. planeta Merkur má dnes excentricitu cca 0.206, její hodnota ale může kolísat přibližně v mezích 0.121-0.232 (a obdobně kolísá také sklon dráhy). Je nepravděpodobné, že by mohly existovat celočíselné poměry mezi veličinami, které se v čase proměňují (při absenci přímé závislosti těchto změn,…).
Titiovo pravidlo
Titius, Johann Daniel| Titius, Johann Daniel, 1729-1796, německý matematik a fyzik. Zabýval se teoretickou i experimentální fyzikou, specielně termometrií. |
Keplerovy komplikované mnohostěny nahradil (r.1766) J.D.Titius jednoduchým pravidlem - velikost velké polosy (a) vyjádřil jako exponenciální funkci pořadového čísla planety (k):
a ≈ 0.4+0.3*2k [AU]
Pro k=0,1,2,4,5 dává Titiův vzorec přibližné vzdálenosti Venuše, Země, Marsu, Jupitera a Saturna od Slunce.
Po publikování J.E.Bodem (r.1772) v populární astronomické knize se pravidlo stalo známým jako Bodeho zákon. Po objevu Uranu (r.1781) na dráze odpovídající k=6 se soustředila pozornost astronomů na dráhu s k=3 v pásmu mezi Marsem a Jupiterem, kde byla (r.1801) objevena planetka Ceres a posléze i několik dalších menších těles – planetek (asteroidů).
Původní Titiův návrh počítal také se vzdáleností 0.4 AU pro Merkur, v takovém případě však (jak ukázal Charlier) uvedená řada není geometrická, resp. pro Merkur vychází k=-∞.
Bode, Johann Elert| Bode, Johann Elert, 1747-1826, německý astronom. Zabýval se přesností zobrazováním hvězd a souhvězdí do map, vydal hvězdný atlas a knihu o souhvězdích. |
Pro k=-1,-2,… mezi Merkurem a Venuší nebylo žádné těleso nalezeno a tedy pro Merkur Titiova řada selhává.
S.F.Dermott (r.1973) ukázal, že soubor náhodně generovaných period je za určitých podmínek možné pokrýt obdobným pravidlem jako je Titiovo a zpochybnil tak, že by dráhy planet byly na logaritmické stupnici nenáhodné.
RozpadRozpad do dvou řad ... Podle pravidla Armelliniho má být vzdálenost každé planety 1.5k: 0.30, 0.45(Merkur), 0.67(Venuše), 1.00(Země), 1.5(Mars),2.3-3.4(planetky),5.1(Jupiter).
Armelliniho pravidlo pokrývá planety od Merkuru až po Jupiter lépe než pravidlo Titiovo.
S ohledem na předpověď existence řady intramerkuriálních planet (pro k=-3,-4,…), která se nepotvrdila, však i toto pravidlo selhává.
|
Pravidlo |
z |
c1 |
c2 |
k0 |
|
Armellini |
1.5 |
0.0 |
1.0 |
1 |
|
Cameron, Ter-Haaf |
1.69 |
0.0 |
0.225 |
-1 |
|
Blagg, Richardson |
1.728 |
0.0 |
1.0 |
0 |
|
Bélot |
1.883 |
0.28 |
1/214.45 |
-6 |
|
Titius |
2.0 |
0.4 |
0.3 |
1 |
Pokusy o aproximaci mají zpravidla tvar:
a ≈ c1+ c2 zk – k0 [AU]
Pro různá z, c1, c2 a k0 dostáváme Armelliniho, Titiovu a např. také Bélotovu a Cameronovu funkci. Cameronova zpřesňuje hodnotu pro Merkur, Bélotova funkce pro Saturn. Jen Titiova funkce poskytuje rozumné hodnoty až po Uran.
Po objevu Neptunu (r.1846) a Pluta (r.1930) se naskytla možnost analyzovat také vzdálenosti mezi vzdálenějšími tělesy. J.Iglauer (r.1937) publikoval řadu pro Saturn, Uran, Neptun a Pluto pro c=9.99 AU, n=0,1,2,3 ve tvaru:
a ≈ a(Saturn) + c*n [AU]
a pro c1=2.94 c2 =0.27, n=2,3,4,5 ve tvaru:
a ≈ (c1-c2*n)*n² [AU]
Ray Tomes (r.1998) postuloval možnost existence stojatých vln – pro vnější planety s vlnovou délkou (blízkou dvojnásobku Iglauerovy konstanty c) 2*9.8 AU (163 světelných minut) a pro vnitřní planety s vlnovou délkou 2*0.35 AU (5.8 světelných minut).
Podle Charliera respektují Saturnovy měsíce vztah a ≈ 1.5+1.6*1.5k. Tento vztah upravil A.Mohorovičič na a ≈ 1.0+2.0*1.4k , ani ten však nesouhlasí se skutečným rozložením měsíců alespoň tak dobře, jako Titiův vztah s rozložením planet.
Podle V.Gutha a F.Linky jsou poměry vzdáleností Saturnových nepravidelné a neodpovídají hodnotami poměrům zjištěných u planet. Vzhledem k pozorované lepší shodě u měsíců Jupitera i Uranu vyslovují domněnku, že systém Saturnových měsíců nemusí být (až na výjimky Mimas-Tethys, Enceladus-Dione,…) ještě zcela ustálen.
V jiných teoriích (např. F.Graner, B.Dubrulle, 1994) bývá Titiovo pravidlo spojováno s ranným vývojem Sluneční soustavy. Soustavy měsíců pak mohly být v průběhu vývoje náchylnější na změny (některé měsíce planeta mohla ztratit a jiné zase z planetek či komet získat).
Zenger , Václav Karel
| Zenger , Václav Karel, 1830-1908, český matematik, fyzik a astrofyzik, uznávaný experimentátor a vynálezce. Iniciátor české fyzikální terminologie. Provedl expertizu na ochranu Eiffelovy věže před bleskem. |
Zpět k periodám
Původní Pýthagorova myšlenka se netýkala souladu vzdáleností, ale frekvencí (a oběžných period).
K.V.Zenger v pojednání o “elektřině světové“představil teorii v níž periody oběhu vnitřních planet přepočítává na sluneční půl-otáčky (12.6 dne).
K zachování řady (s rozdílem 11-ti půl-otáček)
7 (Merkur), 18(Venuše), 29(Země), 40(?) a 51(Eros) vsunul V.K.Zenger mezi dráhu Země a planetky Eros hypotetickou planetu (s periodou cca 500 dní).
Přibližné periody Jupitera, Saturnu, Uranu a Pluta (12,30,84,248 let) připomínají mocniny čísla 3 (9,27,81,243) zvýšené o 3, Neptun zapadá do tohoto schematu hodnotou 2*81+3 (165 let). Nabízí se tedy vztah:
T ≈ r + s*3k-2 [let]
kde r=0 pro vnitřní a r=3 pro vnější planety a s =1 nebo 2. Dvojice (k,s) odpovídají přibližně pro (0,2) Merkuru, (1,2) Venuši, (2,1) Zemi, (2,2) Marsu, (4,1) Jupiteru, (5,1) Saturnu, (6,1) Uranu, (6,2) Neptunu a (7,1) Plutu. (Extrapolace za známé hranice nabízí periody (7,2)=486 let, (8,1)=729 let, (8,2)=1458 let, (9,1)=2187 let apod.)
T ≈ 2k/2(2k+2)/6 ≈ 23k/2/6 [let]
Z Titiova pravidla pro vzdálenosti vychází podle třetího Keplerova zákona (tj. po umocnění na 3/2) přibližně vztah:
(Extrapolací pro k=8 je cca 685 let, pro k=9 cca 1935 let).
Pro soustavy satelitů planet bývá uváděno tzv. Dermottovo pravidlo, podle kterého
se odvozují periody měsíců jako funkce rotační periody centrálního tělesa.
T ≈ c*T0k [dní]
Pokusy o zobecnění
Mary A.Blagg (1913) se pokusila výpočty založenými na vztahu
a ≈ c1+ c2 zk [AU]
pokrýt nejen systém planet ale i satelitní systémy Jupitera, Saturnu a Uranu.
Ve snaze o co nejlepší pokrytí známých dat pro hodnotu c1 stanovila komplikovaný výpočet (obsahující goniometrické funkce,…)
Mohorovičič , Andrija| Mohorovičič , Andrija, 1857-1936, chorvatský geofyzik. Zabýval se zemětřeseními, objevil diskontinuitu rychlostí seizmických vln. |
A.Mohorovičič (1938) upravil Titiovo pravidlo na tvar:
a ≈3.363± 3.363*0.88638k [AU]
čímž se pokusil postihnout i některé známé planetky a komety. Mohorovičič stanovil několik základních podmínek, které by správný vztah měl mít, např. měl by pokrývat i Slunce a stabilní dráhy planetek a komet (tělesa s proměnlivou dráhou nemusí vztah pokrývat,…).
Podle Mohorovičičova pravidla je největší výskyt těles ve vzdálenosti cca 3.363 AU, tj. v pásmu planetek a na obě strany z tohoto místa počet sfér klesá. Pro vnitřní systém planet (do kterého se mezi Mars včleňují planetky Hermes a Eros) a pro planetky mezi Marsem a Jupiterem tak vychází Mohorovičičův návrh v celku přijatelně, pro vnější planety však vznikají sféry s čísly 5 (Jupiter), -5 (Saturn), -13 (Uran) a -17 (Neptun),…
Výsledkem snah M.A.Blagg i Mohorovičových snah je poměrně rozsáhlý soubor drah, který ale nepokrývá celou rozmanitost Sluneční soustavy.
Kvantová mechanikaJ.M.Barnothy se pokusil (r.1947) modifikovat kvantovou mechaniku tak, aby byla použitelná i v makroskopickém měřítku. Vycházel z předpokladu, že tzv.Schrödingerova konstanta závisí na hodnotě spinu, tj. na rotaci sledovaných objektů.
Ve snaze sjednotit Bohrovu a Keplerovu teorii nahradil (r.1973) Schrödingerovu konstantu ћ=h/2π funkcí ћ ≈ 2s/αk, kde s je hodnota spinu a α konstanta jemné struktury (α ≈ 1/137.0). Nejrychleji rotující planety (Jupiter,Saturn) získávají kvantové číslo k=2, jejich sousedé (Uran, Neptun, Mars, Země) k=3 a okrajová tělesa (Merkur, Venuše, Pluto) k=4. Pro svět atomů je k=0 a pro Sluneční soustavu (jako celek obíhající okolo centra galaxie) k=6.
Vyslovil domněnku, že náhlé změny frekvence některých pulzarů (Crab, Vela) mohou být vysvětleny přeskoky z vyšší kvantové hladiny na nižší. (S podobnou myšlenkou vystoupil také I.Velikovskij, při pokusu obhájit svoji domněnku, že Venuše se dostala do Sluneční soustavy teprve nedávno.)
G.V.F.MacDonald (r.1963) a F.F.Fish (r.1967) se soustředili na vztah úhlového momentu a hmotnosti planety. J.P.Bagby (r.1979) publikoval porovnání Titiova pravidla s Bohrovým modelem atomu. Na tyto snahy navázal J.L.Porter a odvodil ve své vlnové mechanice kvantová čísla z momentu hustoty μ=ρ a², kde ρ=M/r³. (V logaritmické stupnici našel v závislosti momentu hustoty na pořadovém čísle planety dva body zlomu – jeden v oblasti Marsu, druhý v místě Saturna).
Čečelnickij navrhl v teorii tzv.astrodynamické spektroskopie vrstvení drah planet, planetek i soustav měsíců planet podle hodnoty účinku L=[Ka(1-ε²)]1/2 .
Za základní kvantum (sfér kL1,k=1,2,3,…) položil pro vnitřní planety L1=L(Merkur)/3 = 0.924 km²/s a pro vnější planety L1=L(Jupiter)/3 = 3.388 km²/s. Mezi Saturnem a Uranem tak získal prostor pro ještě jednu sféru (cca 13.7 AU, Chiron).
Pokusy o exaktní řešení
Podle V.Gutha a F.Linky (1947) není možné, aby pravidelnost odstupů planet i řady měsíců byla náhodná. Vzdálenosti vyplývají ze vzájemného gravitačního působení ústředního tělesa a těles kolem něho obíhajících. Vnitřní souhra gravitačních sil působí, že se vzdálenosti těles po určitém čase ustálí v hodnotách popsatelných nějakým matematickým vztahem.
M.W.Ovenden (r.1972) naznačil možnost vysvětlení Bodeho zákona dynamicky – sousední planety nemohou být příliš blízko. Jak mají být planety minimálně daleko může záviset na jejich hmotnostech (čímž by se vysvětlily i pozorované rozdíly vzdáleností menších vnitřních planet a větších vnější planet).
Hudba a planeta XV analogii astronomie a hudby - vzdálenější planeta představuje hlubší tón. Náš vjem tónů je úměrný logaritmu skutečných frekvencí i skutečných amplitud znění. Čím jsou tóny (v logaritmickém měřítku) blíže k sobě, tím vice si překáží. Obdobně se to zdá být i s planetami (viz Titiovo pravidlo) – vzdálenější planety musí být od sebe dále než bližší… Hlubší tóny jsou zároveň pociťovány jako mohutnější – a také vnější planety jsou mohutnější než planety vnitřní. Můžeme čekat daleko od Slunce planetu větší než je Jupiter???
Uspořádání těles
Tělesa v soustavách jsou buď rovnocenná, např. dvojhvězdy (jako kovalentní vazba v chemii,...) nebo je některé z těles výraznější (hmotnější) a určuje chování jiných těles (iontová vazba,...).
Sluneční soustava je soustava s výrazným centrálním tělesem Sluncem a několika podružnými centry.
Kirkwood Daniel| Kirkwood Daniel, 1814-1889, americký matematik a astronom, studoval dráhy asteroidů a rotační periody planet. Podrobně prozkoumal některé mezery v pásmu planetek mezi Marsem a Jupiterem. |
Skutečnost, že planety utvářejí dvojice pozoroval mezi prvními D.Kirkwood (1852)
Podle velikosti, hustoty, rotační periody i vzdálenosti těžiště od Slunce drží při sobě dvojice Jupiter-Saturn i Uran-Neptun.
Podle vzdálenosti těžiště a velikosti (hustoty) tvoří dvojici také Venuše-Země a Merkur-Mars; jen rotační perioda a vzdálenost od Slunce upřednostňují spíše párování Merkur-Venuše a Země-Mars.
Dráhy dvojic planet, jejichž rotační periody jsou přibližně shodné (Země-Mars, Jupiter-Saturn, Uran-Neptun) jsou ve skutečnosti k sobě blíže, než předpovídá Titiovo pravidlo.
Typy uspořádání
Podle postavení menšího tělesa vzhledem k většímu (a centrálnímu) tělesu rozlišíme dva typy uspořádání:
Nejlehčí uvnitř
Centrální - Menší - Větší
+----+
| | +---+
| | +-+ | |
+----+ +-+ +---+
· Slunce - Merkur - Venuše - Země - Jupiter
· Jupiter - Io - Europa - Ganymed
· Saturn - Mimas - Enceladus - Tethys - Dione - Rhea - Titan
· Uran - Miranda - Ariel - Titan
· Země – umělé satelity -Měsíc
Centrální - Větší - Menší
+----+
| | +---+
| | | | +-+
+----+ +---+ +-+
· Slunce - Jupiter- Saturn - Neptun - Pluto
· Jupiter - Ganymed- Kallisto
· Saturn - Titan - Japetus
· Uranus - Titania- Oberon
· Mars - Phobos - Deimos
Výjimkami z těchto schémat jsou:
- tělesa na téže dráze, např. Slunce-Trojané/Jupiter, Saturn-Helene/Dione
- tělesa přiblišně stejné velikosti např. Slunce-Venuše/Země
Tělesa podle ovlivnění
V závislosti na vzdálenosti od svého centra a vzdálenosti od centra nadřazené soustavy
bývají rozlišovány následující případy:
- Tělesa blízká centru (Mars: Phobos, Deimos, Jupiter: nejbližší měsíce)
- Tělesa rušená jinými tělesy (Laplaceova resonance,…)
- Tělesa rušená centrem soustavy (vzdálené měsíce Jupitera,…)
Symetrie pohybu
Pohyb geometrických os
Geometrická osa
Uvažujme pohyb dvou těles P,Q okolo centra S a pohyb myšlené
(geometrické, neorientované) osy úhlu PSQ. V okamžiku konjunkce planet
P-Q splývá osa s přímkami S-P i S-Q. Za čas t urazí první přímka úhel t/P
(∙360°) a druhá t/Q (∙360°).
Osa těchto přímek po čase t svírá s výchozí přímkou úhel:
t/Q+(t/P-t/Q)/2 = t/Q+t/(2P)-t/(2Q) = t ∙(1/(2P)+1/(2Q)) (∙360°).
Osová perioda dvou těles
 Osová perioda je perioda po
které osa úhlu P-S-Q splyne se svojí původní polohou. Osová perioda dvou
orbitálních period P, Q je perioda:
Osová perioda je perioda po
které osa úhlu P-S-Q splyne se svojí původní polohou. Osová perioda dvou
orbitálních period P, Q je perioda:
[P,Q] = 2/(1/P+1/Q)= 2∙P∙Q/(Q+P)
Osovou periodu značíme hranatými závorkami. Za čas [P,Q] proběhne osa plný úhel 360°.
Pro libovolné periody A,B,C a konstantu k platí:
[A,B] = [B,A][A,A] = A ([A,B],[B,C]) = 2∙(A,C) [k∙A,k∙B] = k∙[A,B]
Při uvažování dvojice planet P,Q a Slunce (Sun) je těžiště
vždy někde uvnitř trojúhelníka SunPQ. Zanedbáme-li rozdíly
v hmotnostech či působení obou planet, můžeme předpokládat, že se
těžiště pohybuje v souladu s osou úhlu PsunQ, tj. s periodou
[P,Q].
Osová perioda více těles
Osová perioda n těles s periodami P,Q,R,S... je určena harmonickým průměrem daných period:
[P,Q,R,S,...] = n/(1/P+1/Q+1/R+1/S...)
Párové osové periody|
Vnějších planet |
Vnitřních planet |
[J,S]= 16.91324 let ( 6177.56 dní)
[J,U]= 20.78898 let ( 7593.18 dní)
[J,N]= 22.13075 let ( 8083.26 dní)
[S,U]= 43.62101 let (15932.57 dní)
[S,N]= 49.97918 let (18254.89 dní)
[U,N]=111.29089 let (40649.00 dní)
|
[M,V]=0.346170 let (126.4385 dní)
[M,E]=0.388199 let (141.7896 dní)
[M,R]=0.427013 let (155.9666 dní)
[V,E]=0.761766 let (278.2351 dní)
[V,R]=0.927141 let (338.6381 dní)
[E,R]=1.305775 let (476.9343 dní)
|
Symetrické konfigurace
Konfigurace více těles je osově symetrická, když dojde ke ztotožnění jistých os pohybu v jednu jedinou. V případě sudého počtu těles nastává taková situace tehdy, když se vyrovnají všechny osy zvolených párů těles. K vyrovnání dvou os může dojít v úhlu 0° nebo 180°, tedy perioda zákrytu činí polovinu synodické periody počítané z period těchto os.
Vnější planety
Čtyři vnější planety sluneční soustavy zaujímají symetrické konfigurace s periodami:
- ([J,S],[U,N])/2 = (16.9132418,111.2908942)/2 = 19.94423/2 let = 9.97212 let
- ([J,U],[S,N])/2 = (20.7889842, 49.9791756)/2 = 35.59471/2 let = 17.79735 let
- ([J,N],[S,U])/2 = (22.1307494, 43.6210092)/2 = 44.92108/2 let = 22.46054 let
Datum (Odstup) Matem.datum
-------------------------------------
2014 Jun 10 AD ( 9.69) 2014.45 JS-UN
2024 Aug 30 AD (10.22) 2024.67
2034 Jul 20 AD ( 9.89) 2034.56
2044 Aug 31 AD (10.12) 2044.67
-------------------------------------
2018 May 6 AD (18.56) 2018.35 JU-SN
2036 Feb 23 AD (17.80) 2036.15
-------------------------------------
2023 May 29 AD (22.08) 2023.41 JN-SU
2046 Jul 13 AD (23.12) 2046.54
Mayská perioda tzolkin (z) v symetrických konfiguracích (jako kvantum):
|
Symetrické konfigurace |
Mayská perioda (násobek tzolkin) |
Poznámka |
|
([J,S],[U,N]) = 19.944 let= 7284.6 dní |
7280 dní = 28*z= 20*364 dní = 260*28 dní (260 přirozených měsíců) 7280 dní = 21*346.67 dní (cca 21 ekliptických let) |
(J,S)= 7253.5 dní= 19.86 let |
|
([J,U],[S,N]) = 35.594 let= 13001 dní |
13000 dní=50*z= 35.59 let 12997.8 dní =3*J = 35.59 let |
(S,N)= 13101.5 dní = 35.87 let. |
Pohyb os vnitřních planet měřený k pohybu osy [J,S] dává periody (n² násobky kvanta q=16.2 dní):
([M,V], [J,S]) = ( 63.219, 3089.0) = 64.540 d (2²*q) ([V,E], [J,S]) = (139.118, 3089.0) = 145.679 d (3²*q) ([E,R], [J,S]) = (238.470, 3089.0) = 258.420 d (4²*q) ~ tzolkin.Perioda (V,E)= 583.92 d (6²*q).
Inverzní pohyb
Periodická symetrie
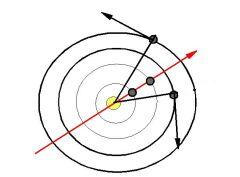
Mějme přímku r pohybující se s periodou R okolo centra. Vzhledem k přímce r se tělesa P a Q pohybují inverzně (protipohybem) tehdy, když r je orientovaná osa pohybu těchto dvou těles, tj. když R=[P,Q].
Tělesa rozevírají a pak přivírají úhel vzhledem k r se synodickou periodou (P,Q).
Představme si nyní, že není nutnou podmínkou, aby tento pohyb probíhal spojitě. Nechť je podmínka inverze splněna ve všech okamžicích t = k∙T, kde k je celé číslo a T nějaká perioda. V těchto okamžicích t musí platit:
Lp - Lr = Lr - Lq
kde Lp,Lq a Lr jsou úhlové délky těles P,Q a Lr je úhlová délka
přímky r. Tedy
frac(T/P)-frac(T/R) = frac(T/R)-frac(T/Q), tj. 2∙frac(T/R) = frac(T/P)+frac(T/Q)
Planety Uran a Neptun vykonávají přibližný inverzní pohyb vzhledem k místům konjunkcí Jupitera se Saturnem.
Za čas t = (J,S) = 19.859 let se změní poloha vnějších planet v průměru o následující úhly: Planeta Úhlová délka Jupiter LJ= frac((J,S)/J)∙360° = 242.7° Saturn LS= frac((J,S)/S)∙360° = 242.7° Uran LU= frac((J,S)/U)∙360° = 85.1° Neptun LN= frac((J,S)/N)∙360° = 43.4°
Rozdíly úhlových délek činí:
LJ - LU = 242.7*360°-85.1*360° = +157.6°
LN - LJ = 43.4*360°-242.7*360° = -199.3*360° = +160.7°
Odchylka je cca 160.7∙360°-157.6∙360° = 3.1°. Úhel 3.1° za 19.859 let odpovídá 360° za cca 2320 let.
Inverzní pohyb U a N vzhledem k (J,S) je modulován periodou H, H je cca 2320 let.
Osové periody vnějších planet: [J,S,U] = 23.04990 let, [J,S,N] = 24.13135 let, [J,U,N] = 29.33301 let, [S,U,N] = 57.78284 let
[J,S,U,N] = 29.36395 let. Osy [J,U,N] a [J,S,U,N] se pohybují s periodou blízkou Saturnově periodě, perioda [S,U,N] dosahuje přibližně dvojnásobku těchto period. Platí: [J,U,N] = [S,3H], [J,S,U,N] = [S,4H], viz Stabilní resonance/Perioda H..
Těžišťové periody
Dvě tělesa (dvojvězdy) obíhají kolem společného těžiště se stejnou
periodou.
V případě více těles se situace komplikuje.
Při oběhu 2 planet okolo Slunce leží těžiště (zanedbáme-li rozdíl v
hmotnostech planet) vždy přibližně na geometrické ose spojnic těchto
těles - viz osová perioda. S osovou periodou se ale pohybuje těžiště
pouze v blízkosti konjuncí planet.
Při opozici planet dochází k "singularitám". V okamžiku singularity se fyzikálně neděje nic zvláštního - překmitne orientace osy. Pohyb těžišťových os tímto připomíná spíše vlnové chování atomu, než jednoduchý cyklický pohyb s pevnou periodou.
Nepravidelný pohyb os
Úhlová rychlost pohybu těžiště kolísá, pohyb reálných orientovaných těžišťových os je nepravidelný.
V okamžiku opozice dojde k "přepólování" - tj. k náhlé změně směru osy. Pohyb těžišťové osy se zpomalí a pak se změní směr od cetrálního tělesa k těžišti o 180º. Tyto „singularity“ ztěžují výpočet průměrné periody pohybu orientovaných os.
Výpočet "okamžitých period" v konjunkcích
dx = dx1m1+dx2m2 /
(m1+m2),
kde dxi =
ai cos dϕi, dyi = ai
sin dϕi, dϕi = dt/Pi
Např. pro Jupiter (J) a Saturn (S), dt=1 rok (po konjunkci J-S),
aJ=5.202 AU, aS = 9.535 AU.
dϕJ = dt/PJ = 30.35°
dxJ = 5.202 * cos(30.35°) = 4.489 AU dyJ =
5.202 * sin(30.35°) = 2.628 AU
dϕS = dt/PS = 12.22°
dxS = 9.535 * cos(12.22°) = 9.319 AU dyS
= 9.535 * sin(12.22°) = 2.018 AU
Σ mi dxi = 317.83*dxJ + 95.16*dxS = 317.83*4.489
+ 95.16*9.319 = 2313.5 [Mzeme*AU]
dxi = 5.60 AU
Σ mi dyi = 317.83*dyJ
+ 95.16*dyS = 317.83*2.628 + 95.16*2.018 =
1027.3 [Mzeme*AU]
dyi = 2.49 AU
tg(dϕ) = dyi / dxi = 2.49 / 5.60 = 0.4446
dϕ = 23.94°
PJS = 1 rok * 360°/23.94° = 15.03 let
Porovnání párových osových period
Porovnání párových osových period s okamžitými párovými periodami v konjunkcích:
|
Periody neorientovaných geometrických os |
"Okamžité periody" počítané v konjunkcích |
[J,S]= 16.91 let
[J,U]= 20.79 let
[J,N]= 22.13 let [J,S,U,N]= 29.36 let
[S,U]= 43.62 let
[S,N]= 49.98 let
[U,N]=111.29 let
|
[J,S]= 15.03 let
[J,U]= 13.49 let
[J,N]= 15.16 let [J,S,U,N]= 19.03 let
[S,U]= 34.73 let
[S,N]= 41.94 let
[U,N]=123.27 let
|
Průměrná perioda těžišťové osy počítané v okamžiku, kdy tělesa leží na jedné polopřímce (tj. jsou v konjunkci) se liší od průměrných period počítaných v jiných výchozích pozicích. Z elementárních úhlových posunů vychází např. perioda cca 15 let v konjunkci J-S, a cca 14 let při kvadratuře J-S.
Reálnou osovou periodu určuje těžší z těles. V okamžiku opozice těles směřuje těžišťová osa k těžšímu z těles. I v okamžiku konjunce tímto tělesem prochází. Tedy reálná těžišťová osa kopíruje - byť nerovnoměrným pohybem - pohyb těžší ze dvou planet.
Minimální interakce
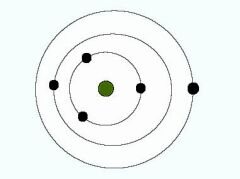
Tělesa pohybující se v soustavách udržovaných gravitační přitažlivostí, paradoxně projevují jakousi "odpudivost". Soustavy se brání kumulaci hmoty na jednom místě. Při delším vzájemném ovlivňování prochází soustava určitým vývojem. Tělesa se nakonec synchronizují a zaujmou jistou optimální a stabilní konfiguraci. Tato konfigurace může -v případě protínajících se drah- vyloučit srážky těles (např. v pohybu planet Neptun a Pluto).
Analytická mechanikaVedle Newtonovy vektorové mechaniky pracující s veličinami, které mají kromě velikosti také směr, vznikala zároveň Leibnitzova analytická mechanika. Analytická mechanika pracuje výhradně jen se skalárními veličinami (hodnotami energií,…), mohla se proto postupně vyčlenit jako čistě matematická věda.
Odpuzování těles
Gravitační přitažlivost těles má jeden poněkud paradoxní důsledek.
Tělesa na drahách (kolem centrálního tělesa) se vzájemně odpuzují. Tento
jev je důsledkem zákona zachování momentu hybnosti (Alfven).
(Elekrony na drahách se také vzájemně odpuzují. Mají stejný
náboj...)
Když se menší těleso pohybuje poblíž většího tělesa (nebo několika
těles), je vystaveno odpudivým silám a nuceno se přizpůsobit. Podle
okolností nastane některá z následujících možností.
Menší těleso se pokusí:
· pohybovat se stejně jako větší těleso (triviální rezonance)
· synchronizovat svůj pohyb s většími tělesy (synchronizační rezonance)
· nasměrovat jinak elipsu své dráhy (rezonance excentricity)
· odklonit rovinu své dráhy jiným směrem (rezonance sklonu)
· změnit směr svého pohybu (zpětný pohyb)
Pokud se ani jedna z možností nezdaří, těleso opouští svoji dráhu (je odhozeno) nebo se rozpadá (je roztrženo).
Princip minimální interakce
Po dlouhodobém vzájemném ovlivňování zaujmou tělesa jistou
optimální konfiguraci a pohybují se tak, že jistá (sumární)
charakteristika nabývá extrému.
(Podle A.M.Molčanova může k takové synchronizaci dojít i při působení
velmi slabých sil.)
Pro některé subsystémy Sluneční soustavy (Io-Europa-Ganymed, měsíce Uranu) byla dokázána platnost Ovendenova principu (t.j. variační princip nebeské mechaniky) [Ovenden,1974]. Pro vnější planety Ovendenův princip selhává.
· Ovenden,1974: Ovenden, M.W., Feagin, T., and Graf, O., "On the Principle of Least Interaction Action and the Laplacean Satellites of Jupiter and Uranus," Celestial Mechanics Journal, 8(4), 455-471 (1974).
Představa principu minimální interakce:
1/ libovolně rozhozená tělesa (rozuměno tělesa na náhodných drahách) se synchronizují (upravují vzájemně fázové posuny na drahách) tak,aby (dlouhodobě) součet jejich interakcí - které jsou nějakou funkcí jejich reálné (nebo úhlové) vzdálenosti a hmotností - byl minimální.
2/ původně náhodné dráhy se (při zachování celkové energie soustavy..) modifikují, aby se ještě dále minimalizovala celková interakce (a na nových drahách se opět upraví fázové posuny podle 1/)
Podle 1/ se chovají Galileovy měsíce, P
Podle 2/ např. poloha Venuše a Země mezi Sluncem a Jupiterem musela postupně upravit nějak tak, aby byla nějaká charakteristika vyvážená?!
UkázkyPřípady jsou rozděleny podle poměrů synodických period vzhledem k jednomu (vnějšímu) "fixovanému" tělesu.
Tři tělesa
Případ 2:1
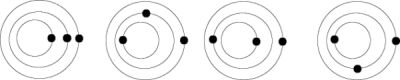
Případ 3:1
(Io-Europa-Ganymed, Miranda-Ariel-Umbriel)

Případ 3:2
(5:2, 7:2, 9:2,...)

Případ 4:3
(8:3,16:3,...)
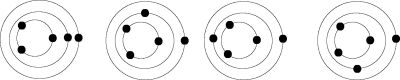
Případ 5:4
(7:4, 9:4, ...)
Planety v rozestupu
18.8.2003
Pozoruhodná konfigurace
Z pohledu minimální interakce - konfigurace planet v období 18.8.2003-31.8.2003 je zajímavá.
Označme V-Venuše, E-Země, R-Mars, J-Jupiter, U-Uran a pozorujme heliocentrické konjunkce a opozice:
18.8.2003 opozice V-E, 21.8.2003 konjunkce V-J, 22.8.2003 opozice E-J24.8.2003 konjunkce E-U27.8.2003 R nejblíže k E, Měsíc v Novu, 28.8.2003 konjunkce R-E30.8.2003 R v přísluní, 31.8.2003 Měsíc v perigeu
Zdá se, jakoby se při této konfiguraci maximalizovaly vzdálenosti:
J-U, J-E, J-R, E-V, R-V, (U-V) ,R-Měsíc.
V okamžiku dlouhodobě největšího přiblížení Marsu k Zemi se sousedící (konkurenční) tělesa Jupiter a Venuše ocitla na opačné straně Sluneční soustavy
V dalším textu vycházíme z opozic planet J-U, r.2003, přesná opozice J-U následovala až 31.10.2003.
Obdobné konfigurace
Některé další obdobné konfigurace najdeme např. v letech 719.29, 1147.48, 1575.66, tj. s přibližně Babylónsko periodou vzhledem k 2003.84: 31*(J,U) = 31*13.8123 let=428.18 let.
Perioda 12J
719 - 862 - 1004,
1147 -1290 - 1433,
1575 - 1718 - 1861,